Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
2.16 Consider this matrix, representing a transformation of R² with respect to the bases. (9) B = (( - ()-(6) D=C). (¹) (a) To what vector in the codomain is the first member of B mapped? 1 2

2.16 Consider this matrix, representing a transformation of R² with respect to the bases. (9) B = (( - ()-(6) D=C). (¹) (a) To what vector in the codomain is the first member of B mapped? 1 2

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question

Please do part A,B,C and please show step by step and explain

✓2.16 Consider this matrix, representing a transformation of R² with respect to the bases. 1 (11) ‹(9)·(1)› D= ‹(1) · (-¹1)› (a) To what vector in the codomain is the first member of B mapped? B Section III. Computing Linear Maps (b) The second member? (c) Where is a general vector from the domain (a vector with components x and y) mapped? That is, what transformation of R² is represented with respect to B, D by this matrix? 229
Transcribed Image Text:✓2.16 Consider this matrix, representing a transformation of R² with respect to the bases. 1 (11) ‹(9)·(1)› D= ‹(1) · (-¹1)› (a) To what vector in the codomain is the first member of B mapped? B Section III. Computing Linear Maps (b) The second member? (c) Where is a general vector from the domain (a vector with components x and y) mapped? That is, what transformation of R² is represented with respect to B, D by this matrix? 229
Expert Solution
Step 1

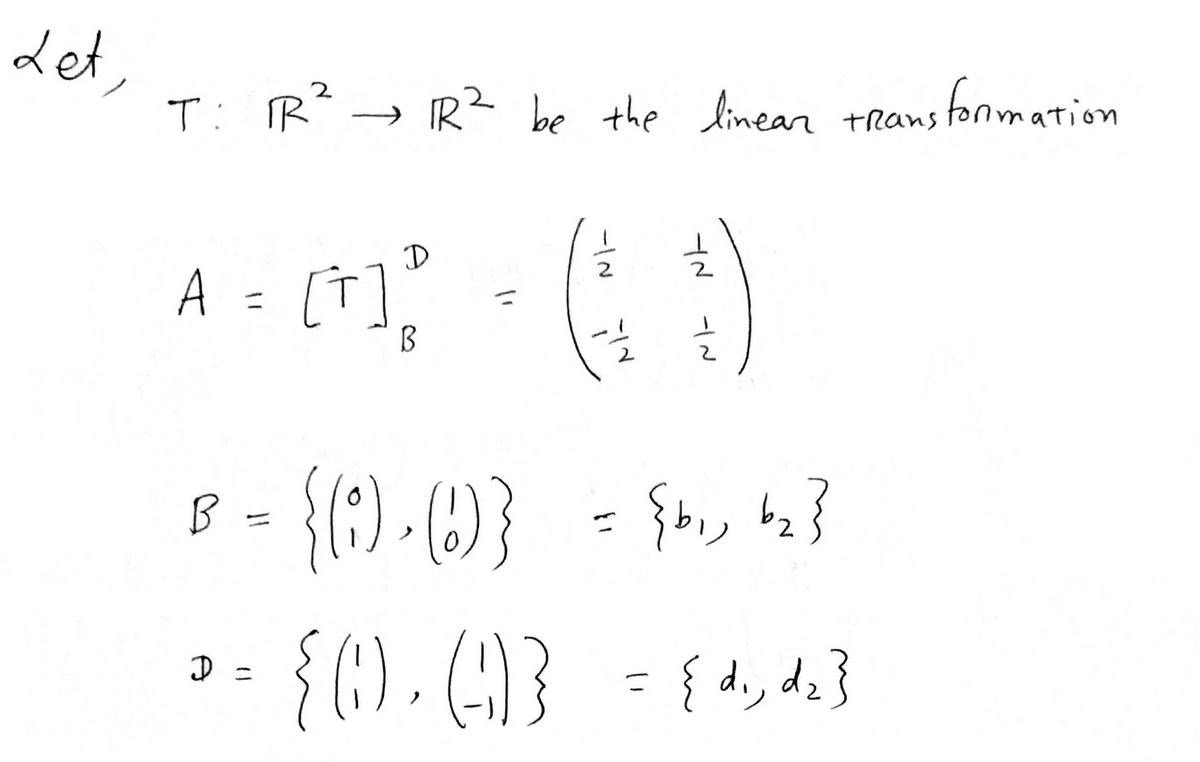
Advanced Math homework question answer, step 1, image 1

trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 3 steps with 3 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS