In the next chapter, on Gauss's law, we will show that a single infinite, flat, uniformly charged sheet creates an electric field that has a magnitude that is the same everywhere, and that this magnitude is |E| σ/(260) where σ = Q/A, the source charge on the sheet divided by the area of the sheet. As you might expect, the field points due to positively charged sheets points away from the sheet and the field of negatively charged sheets points toward the sheet, and so the field due to a particular sheet points opposite directions on the two sides of that sheet. Consider a set of two such sheets, placed parallel to each other. I have labeled three regions: I to the left of both sheets, II between them, and III to the right of both. Suppose that the sheet on the left has a negative surface charge density of -6.0C/m² while the sheet on the right has a positive surface charge density of +9.0C/m². = I 1

The direction of the electric field is away from the positive charge and is towards the negative charge.
(a) The direction of the individual field created in three regions
The electric field due to infinite charge sheet with charge density and the electric field due to infinite charge sheet with charge density .
The diagram below shows the direction of electric field due to infinite charge sheet with charge density
The direction of electric field in region I is in right direction, in region II the direction is towards the negative charge so it is in left direction and the electric field in region III is also towards left direction because the direction of electric field is towards negative charge.
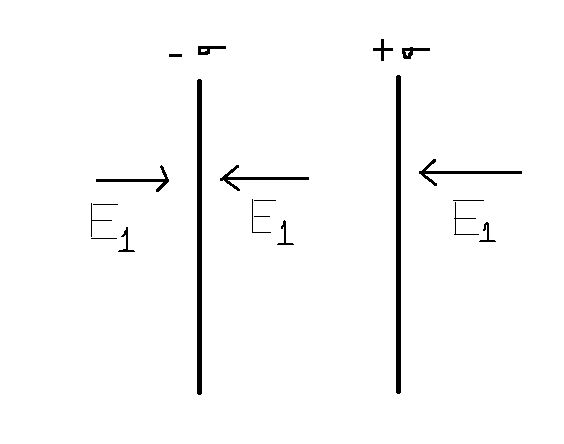
The diagram below shows the direction of electric field due to infinite charge sheet with charge density
The direction of electric field in region I is in left direction, in region II the direction is away from the positive charge so it is in left direction and the electric field in region III is also towards right direction because the direction of electric field is away from positive charge.
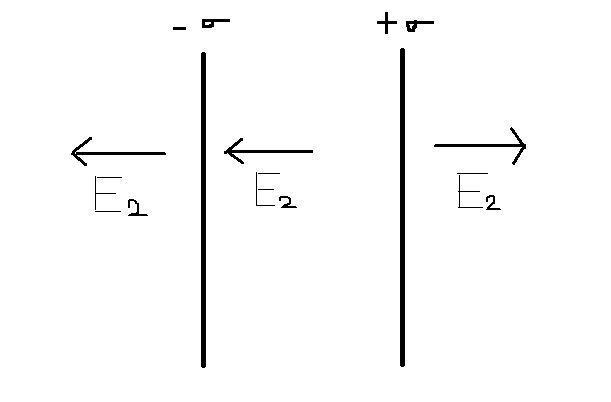
Step by step
Solved in 3 steps with 3 images
