Ina random ample of males, it was found that 23 write with their left lun 217 de . In a random sample of females, it was found that 65 write with their lef and 435 o not (hased on data fiom "The Left-Handed: Their Sinister History," by Fowler Cotas, Education Resources Information Center, Paper 399519). We want to 0.01 sienificance level to test the dlaim that the rate of left-handedness among maies s than that among females a. Tesr the claim usinga hypothesis test. b. Test the daim by construcing an appropriate confidence interval. e. Based on the reults, is the rate of left-handedness among males less than the rate of l handedness among females?

Given that:
| Use left-hand to write? | Male | Female |
| Yes | 23 | 65 |
| No | 217 | 455 |
Significance level,
Find the sample size of each gender by doing sum of "Yes" and "No":
For male, the sample size is:
For female, the sample size is:
Compute the sample proportion for males who write with their left hand by using the formula:
Similarly, compute the sample proportion for males who write with their left hand by using the formula:
(a)
State the null and alternative hypotheses:
This is left-tailed test.
Since this is test of proportions so use z-test or normal distribution.
Compute the pooled proportion by using the formula:
Compute the test statistic:
Determine the critical value at 0.01 significance level by using the following excel function:
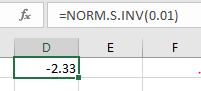
Make Decision:
Rejection rule: Reject H0 if the |calculated test statistic| > |tabulated critical value|, otherwise do not reject it.
Do not reject H0.
Step by step
Solved in 3 steps with 2 images









