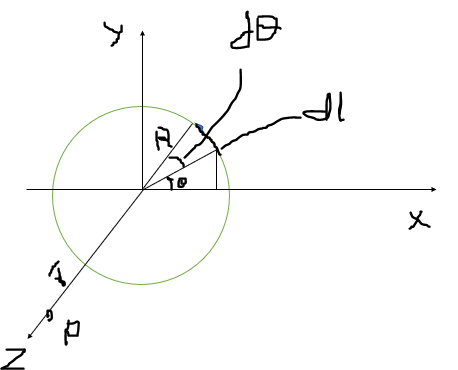
I,j,k are unit vectors in the positive x,y,a direction. What is the electric field at (0,0,h) due to the ring of radius R with the center at (0,0,0) carrying a total charge Q uniformly distributed along its circumference according to Coulomb's Law?

I,j,k are unit vectors in the positive x,y,a direction. What is the electric field at (0,0,h) due to the ring of radius R with the center at (0,0,0) carrying a total charge Q uniformly distributed along its circumference according to Coulomb's Law?

Similar questions

What is the electric field at the center of a sphere of radius R whose volume is uniformly filled with charge (total charge Q)? For this sphere, how does the electric field at a distance r1=R/4 from the center compare to the electric field at a distance r2=3R/4 from the center? Give your answer in the form E(r1)=(some constant)E(r2). For this sphere, how does the electric field at a distance r1=R from the center compare to the electric field at a distance r2=2R from the center? Give your answer in the form E(r1)=(some constant)E(r2).
Which of the following charge distributions will generate a uniform electric field at the specified distance? Select all that apply. a) A distance r from the center of a long, thin line of uniform charge with length L where r << L. b)A distance r away from a large disc of uniform charge (with radius R) where r << R (and not near the edge of the disc) c)A distance r away from a sheet of uniform charge (with dimensions a x a) where r << a (and not near the edge of the sheet). d)Any point between two infinitely large sheets of uniform charge, one with total charge +Q and the other with total charge -Q. e)A distance r from the center of a sphere of uniform charge (with radius R) where r >> R. f)Halfway between two infinitely large sheets of uniform charge, each with total charge -Q.
How would i go about solving this?
An infinitely long conducting cylindrical rod with a positive charge λ per unit length is surrounded by a conducting cylindrical shell (which is also infinitely long) with a charge per unit length of −2λ and radius r1, as shown in the figure. A) What is E(r), the radial component of the electric field between the rod and cylindrical shell as a function of the distance r from the axis of the cylindrical rod? Express your answer in terms of λ, r, and ϵ0 the permittivity of free space. B) What is σ inner, the surface charge density (charge per unit area) on the inner surface of the conducting shell? C) What is σ outer, the surface charge density on the outside of the conducting shell? (Recall from the problem statement that the conducting shell has a total charge per unit length given by −2λ D) What is the radial component of the electric field, E(r), outside the shell?
Consider a cube of side a with 8 charges (4 with charge +e and 4 with charge -e) at the 8 corners. a Since there are a total of 8 charges, there are 28 pars. This may seem like a lot of terms to add, but many of the terms are identical. For example, 12 of the pairs are of opposite sign and separated by an edge of the cube (a distance a). Also, 12 of the pairs are of the same sign and separated by a diagonal of one face (a distance √2 a). Finally, 4 of the pairs are of opposite sign and separated by a diagonal of the cube (a distance √3 a). Calculate the total electrostatic potential energy of this configuration by summing over all the pairs of charges. Give your answer as the numerical coefficient of the following expression U= 4²4 Give your answer to 4 significant figures, and make sure you include the proper sign.
Subpart A-C
Consider a thin plastic rod bent into an arc of radius R and angle a. The rod carries a uniformly distributed negative charge -Q. (Note: the diagram may have the incorrect sign.) y α R -Q X What is the x component of the electric field at the origin? (Enter your responses in terms of the symbolic quantities mentioned in the problem. To make things easier, just write the letter "a" for the angle a, and use the Coulomb constant k rather than the unwieldy 1/4no.) Ex = k*Q*sin(a)/(a*R^2) Computer's answer now shown above. Tries 0/6 What is the y component of the electric field at the origin? Ey = k*Q*(1-cos(a))/(a*R^2) Computer's answer now shown above. Tries 0/6 Follow the steps outlined in class and in the textbook: 1. Use a diagram to explain how you'll cut up the charge distribution, and draw the AE contributed by a representative piece of charge at a given location. 2. Express algebraically the contribution each piece makes to each vector component of the electric field. Indicate…
For this question, Figure 2 (see image). Consider the electric field of a disk of radius R and surface charge density σ along the z-axis as: (see image) a) Use this expression to find the electric field of the disk very close to the disk i.e. Z << R such that the disk looks like an infinite plane with surface charge density σ. b) Use a Gaussian cylinder (pill box) to find the electric field of the plate at this limit (Z << R such that the disk looks like an infinite plane), and compare it with your answer from part a.
You have a very (infinitely) long solid conducting cylinder with length L, base radius R, and total charge +Q. (a) Use Gauss’s law to find the electric field vector inside and outside the cylinder. Explain your reasoning. You can give a verbal description of the electric field vector direction. (b) Similar to how we found the electric field outside a conducting sphere to look like that of a point particle, what does the electric field outside the cylinder look like? (c) Would the electric field inside the cylinder stay the same if the cylinder was instead insulating and uniformly charged? Explain why or why not?
A semicircle of radius a is in the first and second quadrants, with the center of curvature at the origin. Positive charge +Q is distributed uniformly around the left half of the semicircle, and negative charge –Q is distributed uniformly around the right half of the semicircle. What are the magnitude and direction of the net electric field at the origin produced by this distribution of charge?
Can someone please help with the following questions? I've attached the pictures below. I appreciate it! For the problem that asks about the meaning of of p0, I already have the answer for that, I just need help with part b.
I am working on this review question and i couldn't come up with the correct solution. I need a well-explained solution so i can understand the solution and leverage this solution to answer more questions like this.