I AM RESUBMITTING THIS QUESTION FOR MORE SUBPARTS. I NEED HELP FROM NUMBER 4 DOWN. THANK YOU. A grocery store manager did a study to look at the relationship between the amount of time (in minutes) customers spend in the store and the amount of money (in dollars) they spend. The results of the survey are shown below. Time 27 22 17 30 17 19 12 23 22 Money 117 72 53 106 66 93 53 83 95 Find the correlation coefficient: r= Round to 2 decimal places. The null and alternative hypotheses for correlation are: H0:H0: ? μ r ρ == 0 H1:H1: ? r ρ μ ≠≠ 0 The p-value is: (Round to four decimal places) Use a level of significance of α=0.05α=0.05 to state the conclusion of the hypothesis test in the context of the study. There is statistically significant evidence to conclude that a customer who spends more time at the store will spend more money than a customer who spends less time at the store. There is statistically significant evidence to conclude that there is a correlation between the amount of time customers spend at the store and the amount of money that they spend at the store. Thus, the regression line is useful. There is statistically insignificant evidence to conclude that there is a correlation between the amount of time customers spend at the store and the amount of money that they spend at the store. Thus, the use of the regression line is not appropriate. There is statistically insignificant evidence to conclude that a customer who spends more time at the store will spend more money than a customer who spends less time at the store. r2 = (Round to two decimal places) Interpret r2 : There is a 73% chance that the regression line will be a good predictor for the amount of money spent at the store based on the time spent at the store. 73% of all customers will spend the average amount of money at the store. Given any group that spends a fixed amount of time at the store, 73% of all of those customers will spend the predicted amount of money at the store. There is a large variation in the amount of money that customers spend at the store, but if you only look at customers who spend a fixed amount of time at the store, this variation on average is reduced by 73%. The equation of the linear regression line is: ˆyy^ = + xx (Please show your answers to two decimal places) Use the model to predict the amount of money spent by a customer who spends 13 minutes at the store. Dollars spent = (Please round your answer to the nearest whole number.) Interpret the slope of the regression line in the context of the question: The slope has no practical meaning since you cannot predict what any individual customer will spend. As x goes up, y goes up. For every additional minute customers spend at the store, they tend to spend on averge $3.54 more money at the store. Interpret the y-intercept in the context of the question: The average amount of money spent is predicted to be $7.63. The y-intercept has no practical meaning for this study. The best prediction for a customer who doesn't spend any time at the store is that the customer will spend $7.63. If a customer spends no time at the store, then that customer will spend $7.63.
Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.
I AM RESUBMITTING THIS QUESTION FOR MORE SUBPARTS. I NEED HELP FROM NUMBER 4 DOWN. THANK YOU.
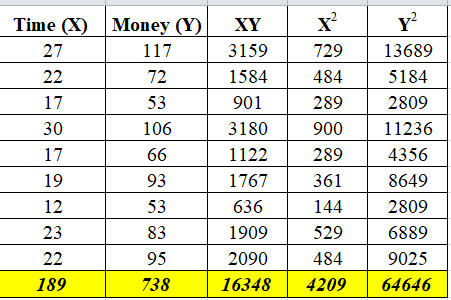
A grocery store manager did a study to look at the relationship between the amount of time (in minutes) customers spend in the store and the amount of money (in dollars) they spend. The results of the survey are shown below.
| Time | 27 | 22 | 17 | 30 | 17 | 19 | 12 | 23 | 22 |
|---|---|---|---|---|---|---|---|---|---|
| Money | 117 | 72 | 53 | 106 | 66 | 93 | 53 | 83 | 95 |
- Find the
correlation coefficient : r= Round to 2 decimal places. - The null and alternative hypotheses for correlation are:
H0:H0: ? μ r ρ == 0
H1:H1: ? r ρ μ ≠≠ 0
The p-value is: (Round to four decimal places) - Use a level of significance of α=0.05α=0.05 to state the conclusion of the hypothesis test in the context of the study.
- There is statistically significant evidence to conclude that a customer who spends more time at the store will spend more money than a customer who spends less time at the store.
- There is statistically significant evidence to conclude that there is a correlation between the amount of time customers spend at the store and the amount of money that they spend at the store. Thus, the regression line is useful.
- There is statistically insignificant evidence to conclude that there is a correlation between the amount of time customers spend at the store and the amount of money that they spend at the store. Thus, the use of the regression line is not appropriate.
- There is statistically insignificant evidence to conclude that a customer who spends more time at the store will spend more money than a customer who spends less time at the store.
- r2 = (Round to two decimal places)
- Interpret r2 :
- There is a 73% chance that the regression line will be a good predictor for the amount of money spent at the store based on the time spent at the store.
- 73% of all customers will spend the average amount of money at the store.
- Given any group that spends a fixed amount of time at the store, 73% of all of those customers will spend the predicted amount of money at the store.
- There is a large variation in the amount of money that customers spend at the store, but if you only look at customers who spend a fixed amount of time at the store, this variation on average is reduced by 73%.
- The equation of the linear regression line is:
ˆyy^ = + xx (Please show your answers to two decimal places) - Use the model to predict the amount of money spent by a customer who spends 13 minutes at the store.
Dollars spent = (Please round your answer to the nearest whole number.) - Interpret the slope of the regression line in the context of the question:
- The slope has no practical meaning since you cannot predict what any individual customer will spend.
- As x goes up, y goes up.
- For every additional minute customers spend at the store, they tend to spend on averge $3.54 more money at the store.
- Interpret the y-intercept in the context of the question:
- The average amount of money spent is predicted to be $7.63.
- The y-intercept has no practical meaning for this study.
- The best prediction for a customer who doesn't spend any time at the store is that the customer will spend $7.63.
- If a customer spends no time at the store, then that customer will spend $7.63.
Note- As you have posted multiple sub parts, so I am providing solutions of three sub parts starting from sub part 4. Kindly resubmit the question for the remaining parts.
Let X be the amount of time (in minutes) customers spend in the store and
Y be the amount of money (in dollars) the customers spend.
The values of x and y are

Number of observations (n) = 9
4. R2 or coefficient of determination

Step by step
Solved in 3 steps with 4 images









