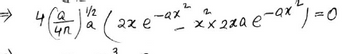Homework Help is Here – Start Your Trial Now!
Science
Advanced Physics
In this question we will cosider the quantum harmonic oscillator . The wavefunction of the first excited state of this system can be written as :  (see figure attached )  where a = mω0 / ħ and A1 and ω0 are real constants . a) Calculate the value of the normalization constant A1 looking up the values of any integrals that you require . State the physical meaning of any condtions you use .  B) Calcuate the values x  at which a physicit observing a particle in this state would have the highest probability of finding it .  C) At which finite of x  is the probability of observing this particle zero?

In this question we will cosider the quantum harmonic oscillator . The wavefunction of the first excited state of this system can be written as :  (see figure attached )  where a = mω0 / ħ and A1 and ω0 are real constants . a) Calculate the value of the normalization constant A1 looking up the values of any integrals that you require . State the physical meaning of any condtions you use .  B) Calcuate the values x  at which a physicit observing a particle in this state would have the highest probability of finding it .  C) At which finite of x  is the probability of observing this particle zero?

icon
Related questions
Question

3. In this question we will cosider the quantum harmonic oscillator . The wavefunction of the first excited state of this system can be written as : 

(see figure attached ) 

where a = mω0 / ħ and A1 and ω0 are real constants .

a) Calculate the value of the normalization constant A1 looking up the values of any integrals that you require . State the physical meaning of any condtions you use . 

B) Calcuate the values x  at which a physicit observing a particle in this state would have the highest probability of finding it . 

C) At which finite of x  is the probability of observing this particle zero?

¥(x, t) = 2A₁√√axe-ax²/2e-³iwot/2 where a = mwo/h, and A₁ and wo are real constants. 9
Transcribed Image Text:¥(x, t) = 2A₁√√axe-ax²/2e-³iwot/2 where a = mwo/h, and A₁ and wo are real constants. 9
Expert Solution
steps

Step by step

Solved in 3 steps with 3 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

Use your answers from parts b) and c) of this question to sketch the probability density of
a particle in this state. Calculate an expression for the position of the turning points of a
classical particle with the same energy as this quantum particle, and indicate the position
of these points on your sketch. 

Solution
Bartleby Expert
SEE SOLUTION
Follow-up Question

How did we get the picture below, through an expansion and if so please show it

→ =o 4 (см)a2 (2х е-а 12 а е 1=0 3 кахае-ах г
Transcribed Image Text:→ =o 4 (см)a2 (2х е-а 12 а е 1=0 3 кахае-ах г
Solution
Bartleby Expert
SEE SOLUTION
Similar questions