For both of the following equations, identify if they are used for adding capacitors in series, in parallel, or neither: a) Ceg = C1 + C2 +.. b) Cag = C + +C++ c) Cq = (& + à +) -1 d) Ceq = (C1 +C2 + ---)~'
Please solve all parts

A capacitor is an arrangement of conductors separated by an insulator (dielectric)used to store charge or introduce reactance into an alternating -current circuit. They are widely used as parts of electrical circuits in many common electrical devices. Capacitance is related to charge and voltage as . Several capacitors may be connected together for different applications. There are two simple and common types of connections, called series and parallel, for which we can easily calculate the total capacitance. Certain more complicated connections can also be related to combinations of series and parallel.
a) Consider three capacitors connected in parallel as shown
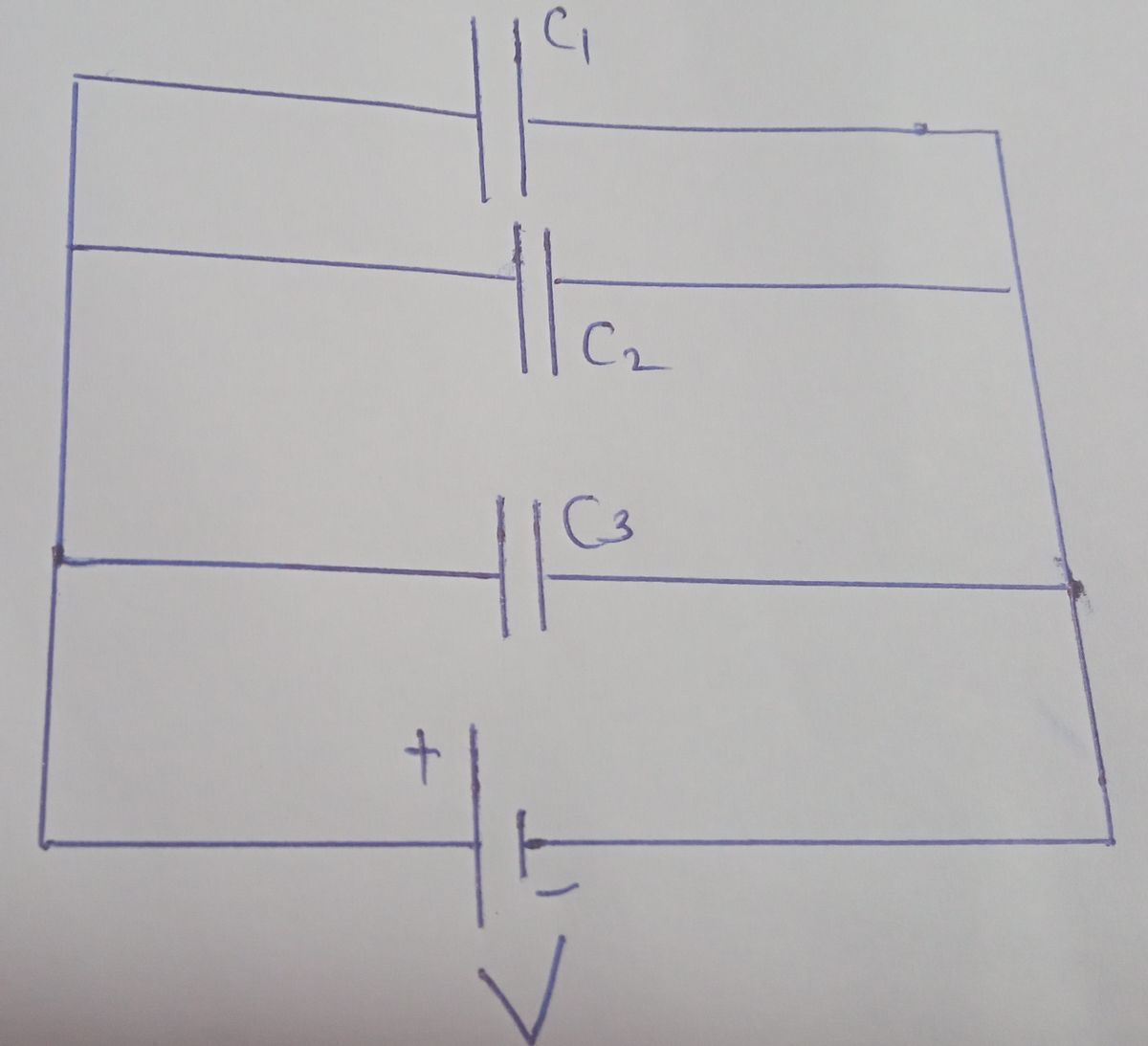
Capacitance
The voltage across each capacitor is V, the same as that of the source since they are connected directly to it through a conductor. (Conductors are equipotentials, and so the voltage across the capacitors is the same as that across the voltage source.) Thus the capacitors have the same charges on them as they would have if connected individually to the voltage source. The total charge Q is the sum of the individual charges: Q = Q1 + Q2 + Q3.
Here, we use the relation
And
Therefore total charge Q can be written as
The above equation is applicable to any number of capacitors.
Hence the expression in option (a) is used for adding capacitors connected in parallel combination.
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 2 images









