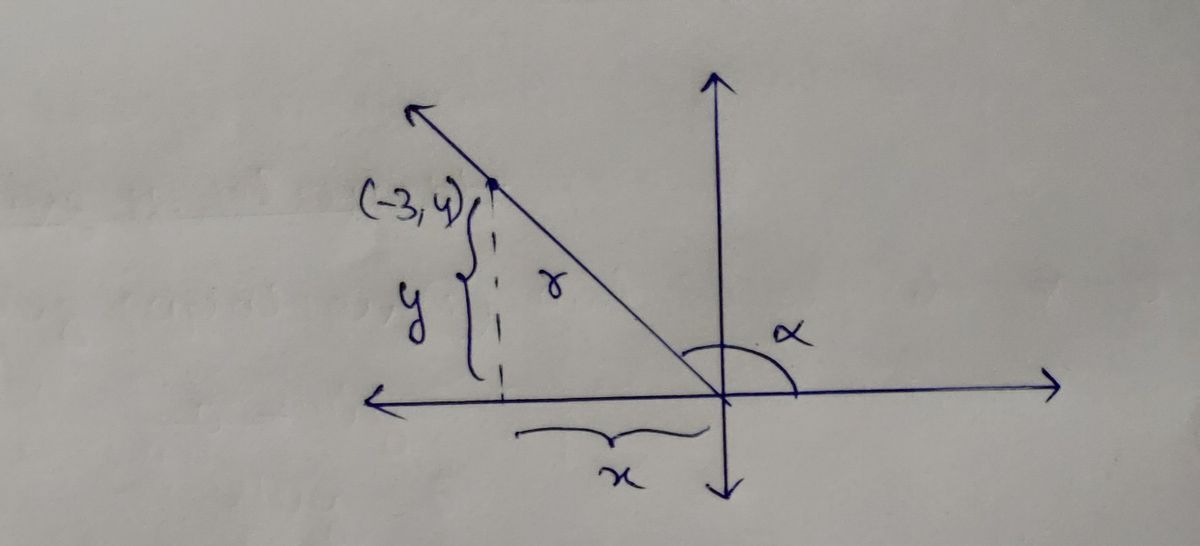
Find sin a. (-3, 4) sin a = [? r
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
![The image is a mathematical problem asking to find the sine of an angle, α.
### Description:
- **Text**:
- "Find sin α."
- "sin α = ?"
- **Diagram**:
- There is a coordinate system with axes.
- A point, labeled (-3, 4), is shown in the second quadrant.
- A vector from the origin to the point (-3, 4) is depicted as "r."
- The angle α is formed between the positive x-axis and vector "r."
### Explanation:
To find \( \sin α \) (the sine of the angle α), use the formula for sine in a right triangle:
\[
\sin α = \frac{opposite}{hypotenuse}
\]
For the point (-3, 4):
- The opposite side to angle α is 4 (y-coordinate).
- The hypotenuse "r" can be found using the Pythagorean theorem:
\[
r = \sqrt{(-3)^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\]
Thus,
\[
\sin α = \frac{4}{5}
\]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F6f2c9438-5a89-4288-b691-8fe1dc913be9%2F1254e646-f00a-4bb0-bc1c-90e4e7d0af5c%2Fxaak1vh_processed.png&w=3840&q=75)
Transcribed Image Text:The image is a mathematical problem asking to find the sine of an angle, α.
### Description:
- **Text**:
- "Find sin α."
- "sin α = ?"
- **Diagram**:
- There is a coordinate system with axes.
- A point, labeled (-3, 4), is shown in the second quadrant.
- A vector from the origin to the point (-3, 4) is depicted as "r."
- The angle α is formed between the positive x-axis and vector "r."
### Explanation:
To find \( \sin α \) (the sine of the angle α), use the formula for sine in a right triangle:
\[
\sin α = \frac{opposite}{hypotenuse}
\]
For the point (-3, 4):
- The opposite side to angle α is 4 (y-coordinate).
- The hypotenuse "r" can be found using the Pythagorean theorem:
\[
r = \sqrt{(-3)^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\]
Thus,
\[
\sin α = \frac{4}{5}
\]
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning