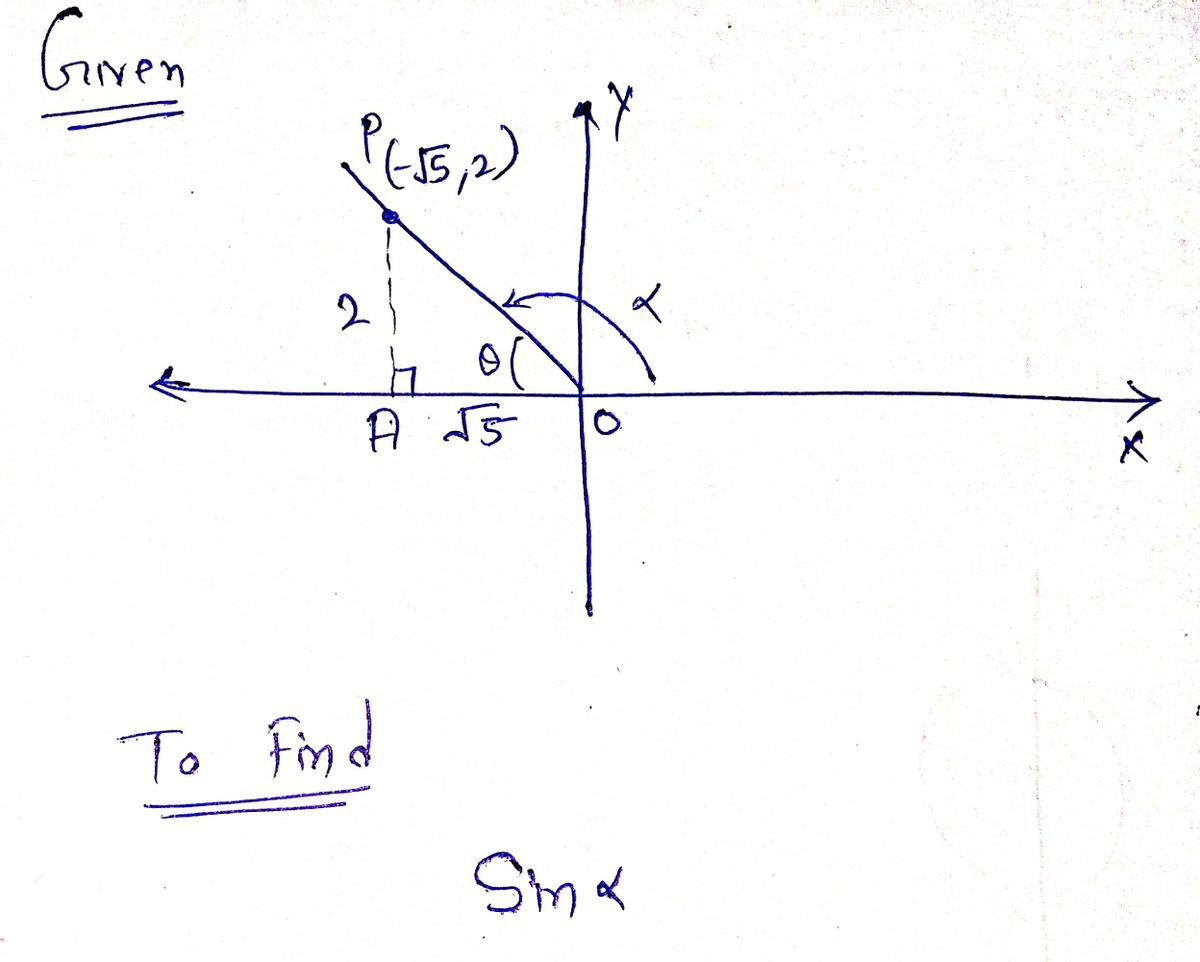
Find sin a. (-/5 ,2) [ ?] 1
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
![**Problem: Find \(\sin \alpha\).**
**Diagram Explanation:**
The graph is on a coordinate grid with a marked point at coordinates \((- \sqrt{5}, 2)\). A line segment extends from the origin (0,0) to this point. The angle \(\alpha\) is formed between this line and the positive x-axis. The point where this line intersects the y-axis at 2 is depicted as one of the coordinates of the point.
The segment's horizontal run is along the x-axis and vertical rise along the y-axis. The hypotenuse, representing the radius of the unit circle, is drawn from the origin to the point \((- \sqrt{5}, 2)\).
The task is to determine \(\sin \alpha\). To compute this, we will use the definition of sine in a right triangle, where \(\sin \alpha = \frac{\text{opposite side}}{\text{hypotenuse}}\).
To find the hypotenuse (\(r\)), we use the coordinates to calculate the distance:
\[
r = \sqrt{(-\sqrt{5})^2 + 2^2} = \sqrt{5 + 4} = \sqrt{9} = 3
\]
Thus, \(\sin \alpha = \frac{2}{3}\).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F6f2c9438-5a89-4288-b691-8fe1dc913be9%2F93c8dd5a-71be-4e27-bd3c-ba60e8f5ffd2%2Fwayx42n6_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem: Find \(\sin \alpha\).**
**Diagram Explanation:**
The graph is on a coordinate grid with a marked point at coordinates \((- \sqrt{5}, 2)\). A line segment extends from the origin (0,0) to this point. The angle \(\alpha\) is formed between this line and the positive x-axis. The point where this line intersects the y-axis at 2 is depicted as one of the coordinates of the point.
The segment's horizontal run is along the x-axis and vertical rise along the y-axis. The hypotenuse, representing the radius of the unit circle, is drawn from the origin to the point \((- \sqrt{5}, 2)\).
The task is to determine \(\sin \alpha\). To compute this, we will use the definition of sine in a right triangle, where \(\sin \alpha = \frac{\text{opposite side}}{\text{hypotenuse}}\).
To find the hypotenuse (\(r\)), we use the coordinates to calculate the distance:
\[
r = \sqrt{(-\sqrt{5})^2 + 2^2} = \sqrt{5 + 4} = \sqrt{9} = 3
\]
Thus, \(\sin \alpha = \frac{2}{3}\).
Expert Solution
Step 1
Step by step
Solved in 4 steps with 3 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning