Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
Can anyone please help me to solve this problem? Please I am stuck!
![**Title: Finding an Equation of a Plane Orthogonal to a Line**
**Introduction:**
In this exercise, we will determine the equation of a plane that passes through a given point and is orthogonal to a specified line. This requires understanding the relationship between planes and lines in three-dimensional space.
**Problem:**
Find an equation of a plane through the point \( (-5, 4, -3) \) which is orthogonal to the line given by the parametric equations:
- \( x = 5t - 1 \)
- \( y = -8t + 5 \)
- \( z = -1 + 3t \)
**Solution Outline:**
1. **Determine the Direction Vector:** The line's parametric equations provide the direction vector of the line. For the given line, the direction vector is \( \langle 5, -8, 3 \rangle \).
2. **Use the Direction Vector as the Normal Vector:** Since the plane is orthogonal to the line, the direction vector of the line will be the normal vector of the plane.
3. **Point-Normal Form of the Plane Equation:** The general equation of a plane in point-normal form is:
\[
a(x - x_0) + b(y - y_0) + c(z - z_0) = 0
\]
where \( \langle a, b, c \rangle \) is the normal vector and \( (x_0, y_0, z_0) \) is a point on the plane.
4. **Substitute the Values:**
- Normal Vector: \( \langle 5, -8, 3 \rangle \)
- Point on the Plane: \( (-5, 4, -3) \)
The plane equation becomes:
\[
5(x + 5) - 8(y - 4) + 3(z + 3) = 0
\]
5. **Simplify the Equation:**
\[
5x + 25 - 8y + 32 + 3z + 9 = 0
\]
\[
5x - 8y + 3z + 66 = 0
\]
**Conclusion:**
The equation of the plane orthogonal to the given line and passing through](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F99d15f92-0bff-4b4d-a47e-2ac33d144271%2Fd8313588-ce77-487d-a381-5edecb292a01%2Fuoq07g_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Title: Finding an Equation of a Plane Orthogonal to a Line**
**Introduction:**
In this exercise, we will determine the equation of a plane that passes through a given point and is orthogonal to a specified line. This requires understanding the relationship between planes and lines in three-dimensional space.
**Problem:**
Find an equation of a plane through the point \( (-5, 4, -3) \) which is orthogonal to the line given by the parametric equations:
- \( x = 5t - 1 \)
- \( y = -8t + 5 \)
- \( z = -1 + 3t \)
**Solution Outline:**
1. **Determine the Direction Vector:** The line's parametric equations provide the direction vector of the line. For the given line, the direction vector is \( \langle 5, -8, 3 \rangle \).
2. **Use the Direction Vector as the Normal Vector:** Since the plane is orthogonal to the line, the direction vector of the line will be the normal vector of the plane.
3. **Point-Normal Form of the Plane Equation:** The general equation of a plane in point-normal form is:
\[
a(x - x_0) + b(y - y_0) + c(z - z_0) = 0
\]
where \( \langle a, b, c \rangle \) is the normal vector and \( (x_0, y_0, z_0) \) is a point on the plane.
4. **Substitute the Values:**
- Normal Vector: \( \langle 5, -8, 3 \rangle \)
- Point on the Plane: \( (-5, 4, -3) \)
The plane equation becomes:
\[
5(x + 5) - 8(y - 4) + 3(z + 3) = 0
\]
5. **Simplify the Equation:**
\[
5x + 25 - 8y + 32 + 3z + 9 = 0
\]
\[
5x - 8y + 3z + 66 = 0
\]
**Conclusion:**
The equation of the plane orthogonal to the given line and passing through
![**Problem:**
Find an equation of a plane through the point \((-5, 4, -3)\) which is orthogonal to the line:
\[ x = 5t - 1 \]
\[ y = -6t + 4 \]
\[ z = -1(t + 3t) \]
**Solution Explanation:**
To find the equation of a plane that passes through a given point and is orthogonal to a line, you need to determine the direction vector of the line and use it as the normal vector for the plane.
1. **Find the direction vector of the line**:
- From the parametric equations of the line, the coefficients of \(t\) in each equation represent the direction vector. So, the direction vector \(\mathbf{d}\) is \((5, -6, -1)\).
2. **Use the direction vector as the normal vector of the plane**:
- The general equation of a plane with a normal vector \((a, b, c)\) passing through a point \((x_0, y_0, z_0)\) is:
\[ a(x - x_0) + b(y - y_0) + c(z - z_0) = 0 \]
3. **Substitute the given point and normal vector into the plane equation**:
- For the point \((-5, 4, -3)\) and normal vector \((5, -6, -1)\):
\[ 5(x + 5) - 6(y - 4) - 1(z + 3) = 0 \]
4. **Simplify the equation to find the plane through the given point**:
- Expand and simplify the equation:
\[ 5x + 25 - 6y + 24 - z - 3 = 0 \]
\[ 5x - 6y - z + 46 = 0 \]
Thus, the equation of the plane is \(5x - 6y - z + 46 = 0\).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F99d15f92-0bff-4b4d-a47e-2ac33d144271%2Fd8313588-ce77-487d-a381-5edecb292a01%2Fc15ldxl_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem:**
Find an equation of a plane through the point \((-5, 4, -3)\) which is orthogonal to the line:
\[ x = 5t - 1 \]
\[ y = -6t + 4 \]
\[ z = -1(t + 3t) \]
**Solution Explanation:**
To find the equation of a plane that passes through a given point and is orthogonal to a line, you need to determine the direction vector of the line and use it as the normal vector for the plane.
1. **Find the direction vector of the line**:
- From the parametric equations of the line, the coefficients of \(t\) in each equation represent the direction vector. So, the direction vector \(\mathbf{d}\) is \((5, -6, -1)\).
2. **Use the direction vector as the normal vector of the plane**:
- The general equation of a plane with a normal vector \((a, b, c)\) passing through a point \((x_0, y_0, z_0)\) is:
\[ a(x - x_0) + b(y - y_0) + c(z - z_0) = 0 \]
3. **Substitute the given point and normal vector into the plane equation**:
- For the point \((-5, 4, -3)\) and normal vector \((5, -6, -1)\):
\[ 5(x + 5) - 6(y - 4) - 1(z + 3) = 0 \]
4. **Simplify the equation to find the plane through the given point**:
- Expand and simplify the equation:
\[ 5x + 25 - 6y + 24 - z - 3 = 0 \]
\[ 5x - 6y - z + 46 = 0 \]
Thus, the equation of the plane is \(5x - 6y - z + 46 = 0\).
Expert Solution
Step 1
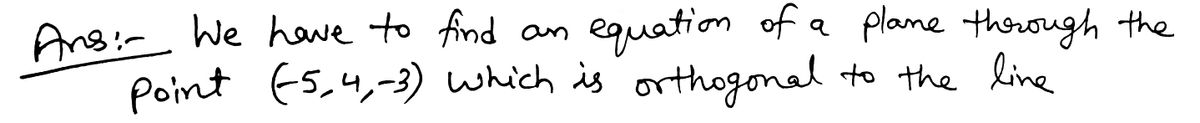
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning