Exercise 4. (a) Two people play a dice game. Each throws a regular 6 sided die. The perso with the largest number wins. (i) What is the probability that they throw exactly the same number (so no-one wins)? (ii) Calculate the probability that player 1 wins in two ways, (1.) using conditional probabilit conditioned on all the possible numbers that player 1 could throw, (2.) by arguing that, given th one player wins, then it must be player 1 or player 2 with equal probability. Check that your tw solution methods yield identical answers.
Exercise 4. (a) Two people play a dice game. Each throws a regular 6 sided die. The perso with the largest number wins. (i) What is the probability that they throw exactly the same number (so no-one wins)? (ii) Calculate the probability that player 1 wins in two ways, (1.) using conditional probabilit conditioned on all the possible numbers that player 1 could throw, (2.) by arguing that, given th one player wins, then it must be player 1 or player 2 with equal probability. Check that your tw solution methods yield identical answers.
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question

Transcribed Image Text:Exercise 4. (a) Two people play a dice game. Each throws a regular 6 sided die. The person
with the largest number wins.
(i) What is the probability that they throw exactly the same number (so no-one wins)?
(ii) Calculate the probability that player 1 wins in two ways, (1.) using conditional probability,
conditioned on all the possible numbers that player 1 could throw, (2.) by arguing that, given that
one player wins, then it must be player 1 or player 2 with equal probability. Check that your two
solution methods yield identical answers.
1
(b) Now suppose that Player 1 is throwing a 4 sided (tetrahedral) die and Player 2 is throwing
a 6 sided (cube) die.
(i) How many possible outcomes are there for Player 1's score and Player's 2 score.
(ii) What is the probability that the two players throw the exact same number.
(iii) Use conditional probability to calculate the probability that Player 1 wins.
Expert Solution
Step 1
Hello! As you have posted 2 different questions, we are answering the first question. In case you require the unanswered question also, kindly re-post them as separate question.
a)
In the given situation,
Two people play a dice game.
Each throws a regular 6 sided die.
The person with the largest number wins.
Let W be the event that the player 1 wins.
A be the event that the outcome of player 1.
B be the event that the outcome of player 2.
The outcomes for throwing two dice are,
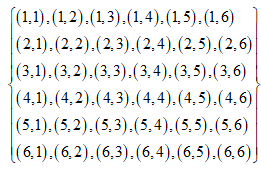
Total outcomes=36
Step by step
Solved in 4 steps with 1 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
