A researcher studies water clarity at the same location in a lake on the same dates during the course of a year and repeats the measurements on the same dates 5 years later. The researcher immerses a weighted disk painted black and white and measures the depth (in inches) at which it is no longer visible. The collected data is given in the table below. Complete parts (a) through ( below Observation 1 2 3 4 5 6 1/25 3/19 5/30 7/3 9/13 11/7 71.2 35.6 53.8 41.2 57.3 43.4 72.1 35.1 59.0 41.0 61.0 47.0 Date Initial Depth, X, Depth Five Years Later, Y, Click the icon to view the table of critical t-values. COO (a) Why is it important to take the measurements on the same date? OA. Using the same dates makes it easier to remember to take samples. OB. Those are the same dates that all biologists use to take water clarity samples. OC. Using the same dates makes the second sample dependent on the first and reduces variability in water clarity attributable to date. OD. Using the same dates maximizes the difference in water clarity.
A researcher studies water clarity at the same location in a lake on the same dates during the course of a year and repeats the measurements on the same dates 5 years later. The researcher immerses a weighted disk painted black and white and measures the depth (in inches) at which it is no longer visible. The collected data is given in the table below. Complete parts (a) through ( below Observation 1 2 3 4 5 6 1/25 3/19 5/30 7/3 9/13 11/7 71.2 35.6 53.8 41.2 57.3 43.4 72.1 35.1 59.0 41.0 61.0 47.0 Date Initial Depth, X, Depth Five Years Later, Y, Click the icon to view the table of critical t-values. COO (a) Why is it important to take the measurements on the same date? OA. Using the same dates makes it easier to remember to take samples. OB. Those are the same dates that all biologists use to take water clarity samples. OC. Using the same dates makes the second sample dependent on the first and reduces variability in water clarity attributable to date. OD. Using the same dates maximizes the difference in water clarity.
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
100%

Transcribed Image Text:**Research on Water Clarity Over Time**
A researcher conducted a study on water clarity at a consistent location in a lake, taking measurements on the same dates each year. After five years, the same measurements were repeated on these dates. The process involved immersing a weighted disk, painted black and white, to determine water depth (in inches) until it was no longer visible. Below is the collected data:
**Table of Observations:**
| Observation | 1 | 2 | 3 | 4 | 5 | 6 |
|--------------|------|------|------|------|------|------|
| Date | 1/25 | 3/19 | 5/30 | 7/3 | 9/13 | 11/7 |
| Initial Depth, \( X_i \) (in inches) | 71.2 | 35.6 | 53.8 | 41.2 | 57.3 | 43.4 |
| Depth 5 Years Later, \( Y_i \) (in inches) | 72.1 | 35.1 | 59.0 | 41.0 | 61.0 | 47.0 |
**Question (a): Importance of Consistent Measurement Dates**
Why is it crucial to measure on the same dates?
A. Using the same dates makes it easier to remember to take samples.
B. Those are the same dates that all biologists use to take water clarity samples.
C. Using the same dates makes the second sample dependent on the first and reduces variability in water clarity attributable to date.
D. Using the same dates maximizes the difference in water clarity.
**Graph/Diagram Explanation:**
There is no graph or diagram included; the focus is on the data table showcasing water clarity measurements over two time periods.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Transcribed Image Text:# Study on Water Clarity Over Time
A researcher examines water clarity at one location in a lake on identical dates over a year and repeats the measurements five years later. Using a weighted disk painted black and white, the depth (in inches) at which the disk is no longer visible is recorded. The collected data is as follows:
| Observation | Date | Initial Depth, \(X_i\) | Depth Five Years Later, \(Y_i\) |
|-------------|--------|------------------------|---------------------------------|
| 1 | 1/25 | 71.2 | 72.1 |
| 2 | 3/19 | 35.6 | 35.1 |
| 3 | 5/30 | 53.8 | 59.0 |
| 4 | 7/3 | 41.2 | 41.0 |
| 5 | 9/13 | 37.5 | 61.0 |
| 6 | 11/7 | 43.4 | 47.0 |
## Questions and Analysis
### (a) Why is it important to take the measurements on the same date?
- **A.** Using the same dates makes it easier to remember to take samples.
- **B.** Those are the same dates that all biologists use to take water clarity samples.
- **C.** Using the same dates makes the second sample dependent on the first and reduces variability in water clarity attributable to date.
- **D.** Using the same dates maximizes the difference in water clarity.
**Correct Answer: C.** Using the same dates ensures that variabilities due to changes in environmental conditions over the year are minimized, making the results more precise.
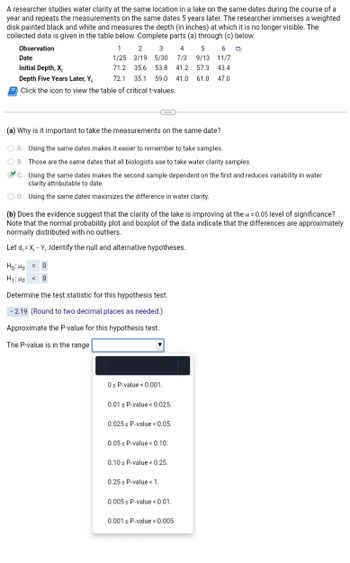
### (b) Does the evidence suggest that the clarity of the lake is improving at the \(\alpha = 0.05\) level of significance?
- **Null Hypothesis (\(H_0\))**: \(\mu_d = 0\)
- The mean difference between the initial and later measurements is zero.
- **Alternative Hypothesis (\(H_1\))**: \(\mu_d < 0\)
- The mean depth is less initially than five years later.
**Test Statistic**: \(-2.19\) (
Solution
Follow-up Question
![**Determine the Test Statistic for This Hypothesis Test**
Please calculate the test statistic needed for this hypothesis test. Ensure your answer is rounded to two decimal places, if necessary.
*Input your value here:*
\[ \_\_ \]](https://content.bartleby.com/qna-images/question/ac3be618-b645-4bd8-855b-808ff3fc18d4/bd565413-47e1-4e23-b951-eca18ed0160a/1isfe2l_thumbnail.png)
Transcribed Image Text:**Determine the Test Statistic for This Hypothesis Test**
Please calculate the test statistic needed for this hypothesis test. Ensure your answer is rounded to two decimal places, if necessary.
*Input your value here:*
\[ \_\_ \]
Solution
Follow-up Question
Transcribed Image Text:**Title: Analyzing Lake Water Clarity Over Time**
A researcher studies water clarity at the same location in a lake on the same dates during the course of a year and repeats the measurements on the same dates 5 years later. The researcher immerses a weighted disk painted black and white and measures the depth (in inches) at which it is no longer visible. The collected data is given in the table below.
| Observation | Date | Initial Depth, X₁ | Depth Five Years Later, Y₁ |
|-------------|--------|------------------|--------------------------|
| 1 | 1/25 | 71.2 | 72.1 |
| 2 | 3/19 | 36.5 | 35.1 |
| 3 | 5/30 | 48.2 | 59.0 |
| 4 | 7/3 | 41.2 | 41.0 |
| 5 | 9/13 | 57.3 | 61.0 |
| 6 | 11/7 | 43.4 | 47.0 |
**Question (a): Why is it important to take the measurements on the same date?**
- **A.** Using the same dates makes it easier to remember to take samples.
- **B.** Those are the same dates that all biologists use to take water clarity samples.
- **C.** Using the same dates makes the second sample dependent on the first and reduces variability in water clarity attributable to date.
- **D.** Using the same dates maximizes the difference in water clarity.
**Correct Answer: C.** Using the same dates makes the second sample dependent on the first and reduces variability in water clarity attributable to date.
**Question (b): Does the evidence suggest that the clarity of the lake is improving at the α = 0.05 level of significance?**
Note that the normal probability plot and boxplot of the data indicate that the differences are approximately normally distributed with no outliers.
Let \( d_i = X_i - Y_i \). Identify the null and alternative hypotheses.
- **H₀:** μ_d = 0
- **H₁:** μ_d ≠ 0
Determine the test statistic for this hypothesis test. (Round to two decimal
Solution
Follow-up Question
![A researcher studies water clarity at the same location in a lake on the same dates during the course of a year and repeats the measurements on the same dates 5 years later. The researcher immerses a weighted disk painted black and white and measures the depth (in inches) at which it is no longer visible. The collected data is given in the table below. Complete parts (a) through (c) below.
| Observation | 1 | 2 | 3 | 4 | 5 | 6 |
|-----------------|-----|-----|-----|-----|-----|-----|
| Date | 1/25 | 3/19 | 5/30 | 7/3 | 9/13 | 11/7 |
| Initial Depth, X₁ | 71.2 | 35.5 | 59.0 | 57.3 | 43.4 | |
| Depth Five Years Later, Y₁ | 72.1 | 35.1 | 59.0 | 61.0 | 47.0 | |
Click the icon to view the table of critical t-values.
**(a) Why is it important to take the measurements on the same date?**
- **A.** Using the same dates makes it easier to remember to take samples.
- **B.** Those are the same dates that all biologists use to take water clarity samples.
- **C.** Using the same dates makes the second sample dependent on the first and reduces variability in water clarity attributable to date. *(Correct Answer)*
- **D.** Using the same dates maximizes the difference in water clarity.
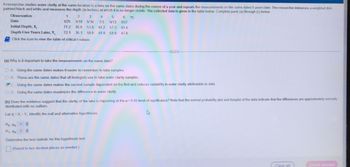
**(b) Does the evidence suggest that the clarity of the lake is improving at the α = 0.05 level of significance?** Note that the normal probability plot and boxplot of the data indicate that the differences are approximately normally distributed with no outliers.
Let's define \( d_i = X_{i} - Y_{i} \). Identify the null and alternative hypotheses.
- **H₀:** μd [Select your answer]
- **H₁:** μd [Select your answer]](https://content.bartleby.com/qna-images/question/ac3be618-b645-4bd8-855b-808ff3fc18d4/dfbb58e9-4509-49d9-8b2d-5c4411d731fd/syvc57h_thumbnail.jpeg)
Transcribed Image Text:A researcher studies water clarity at the same location in a lake on the same dates during the course of a year and repeats the measurements on the same dates 5 years later. The researcher immerses a weighted disk painted black and white and measures the depth (in inches) at which it is no longer visible. The collected data is given in the table below. Complete parts (a) through (c) below.
| Observation | 1 | 2 | 3 | 4 | 5 | 6 |
|-----------------|-----|-----|-----|-----|-----|-----|
| Date | 1/25 | 3/19 | 5/30 | 7/3 | 9/13 | 11/7 |
| Initial Depth, X₁ | 71.2 | 35.5 | 59.0 | 57.3 | 43.4 | |
| Depth Five Years Later, Y₁ | 72.1 | 35.1 | 59.0 | 61.0 | 47.0 | |
Click the icon to view the table of critical t-values.
**(a) Why is it important to take the measurements on the same date?**
- **A.** Using the same dates makes it easier to remember to take samples.
- **B.** Those are the same dates that all biologists use to take water clarity samples.
- **C.** Using the same dates makes the second sample dependent on the first and reduces variability in water clarity attributable to date. *(Correct Answer)*
- **D.** Using the same dates maximizes the difference in water clarity.
**(b) Does the evidence suggest that the clarity of the lake is improving at the α = 0.05 level of significance?** Note that the normal probability plot and boxplot of the data indicate that the differences are approximately normally distributed with no outliers.
Let's define \( d_i = X_{i} - Y_{i} \). Identify the null and alternative hypotheses.
- **H₀:** μd [Select your answer]
- **H₁:** μd [Select your answer]
Solution
Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman