Answered: Determine the acceleration of the block…

Related questions

Question

An 5.2 kg wooden block is held against a wall with force (Fx) = 9.8 N. The friction coefficient between the two surfaces (µ)=0.50. Determine the acceleration of the block if a upward force of 36.0 N is applied. Use positive for an upward acceleration and negative for a downward acceleration.

Expert Solution

Step 1

Newton's Second Law of Motion

According to Newton's Second Law of motion, the rate of change of linear momentum of an object is directly proportional to the external force applied on the object. Mathematically it is represented as

$\sum_{i = 1}^{n} F_{i} = m a$

The LHS is the net external force acting on an object of mass $m$ causing an acceleration of $a$ .

Friction is a retarding force that always acts in a direction opposite to the motion of an object. It is given as

$f = μ N$

$N$ is the normal reaction force and $μ$ is called the coefficient of friction. If the object is stationary then $μ$ is called the coefficient of static friction and if the object is moving then it is called the coefficient of kinetic friction.

Step 2

Given in the question, the mass of the block $m = 5.2 k g$

the force acting on the block towards the right $F_{x} = 9.8 N$

the force acting on the block in upward direction $F_{y} = 36.0 N$ .

the coefficient of friction $μ = 0.5$

the acceleration due to gravity $g = 9.8 m / s^{2}$

Let us draw the free body diagram of the block.

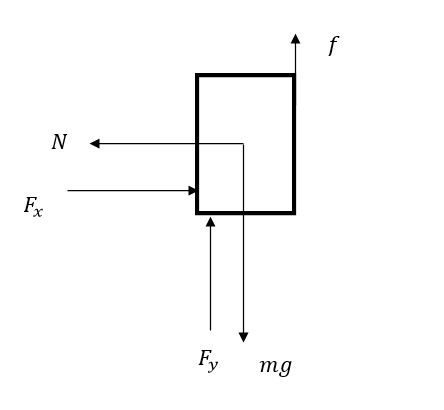
In the diagram, $N$ is the normal reaction force due to the wall, $m g$ is the weight of the block acting downward. Due to the weight of the block, the weight will overpower the applied force and the block will start to move downwards. Thus the frictional force $f$ will be in the upward direction.

Considering the right to be positive and upward to be positive, the net force on the block in the horizontal direction

$F_{1} = F_{x} - N$

Since there is no motion in the horizontal direction then by Newton's Second Law

$F_{x} - N = 0 \Rightarrow N = F_{x}$

Now we know that the frictional force is $f = μ N$

This gives

$f = μ F_{x}$

The net force acting in the vertical direction

$F_{2} = F_{y} - m g + f = F_{y} - m g + μ F_{x}$

If $a$ is the acceleration of the block, then by Newton's Second Law

$F_{y} - m g + μ F_{x} = m a$

Then the acceleration of the block is

$a = \frac{F_{y} - m g + μ F_{x}}{m} = \frac{36 - (5.2 \times 9.8) + (0.5 \times 9.8)}{5.2} m / s^{2} = - 1.93 m / s^{2}$

Step by step

Solved in 3 steps with 1 images

Determine the acceleration of the block if a upward force of 36.0 N is applied.