Determine its average acceleration during the 34.0 sec interval. Average acceleration is given by aavg = v-ut = (6.29 m/s) - (i)(34 s) = aavg = 6.53j^-i^34 aavg = -0.192i^+0.192j^ m/s2
Hi, below is the explanation to the problem cited. But I don't understand the answer to the last question #3: Determine its average acceleration during the 34.0 sec interval. I am lost; can you help? Thanks!
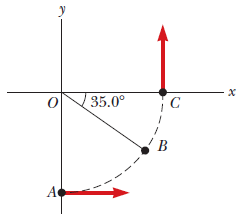
A car initially traveling eastward turns north by traveling in a circular path at uniform speed as in the figure below. The length of the arc ABCis 214 m, and the car completes the turn in 34.0 s.
An x y coordinate system is shown. Three points A, B, and C are shown on the graph. These points are joined by a dotted curve. Point A is on the negative y-axis, point C is on the positive x-axis, while point B is in the fourth quadrant IV at an angle of −35° with the x-axis. From point A the curve initially moves rightward along a circular path, curves upward to cross B and then meets C. An arrow indicating the velocity at point A points horizontally and to the right. An arrow indicating the velocity at point C points vertically upward.
1. What is the acceleration when the car is at Blocated at an angle of 35.0°? Express your answer in terms of the unit vectors î and ĵ.
The turning of car from point A till point C is a case of uniform circular motion where the speed is constant. Since the direction is changing, this means that only centripetal acceleration is acting on the car.
We know that the magnitude of this centripetal acceleration is given by ac = v2 / r where v and r are the values for speed and radius of the circle or circular arc respectively.
Path length or distance covered d=214 m. and time taken t=34 sec
Hence the speed at point B is VB = d / tv = (214m) / (34s) = 6.29 m/s
The radius is calculated as r = 2d / π
r=2d / π
r=(2)(214) / (3.14)
r=136.31 m
The magnitude of acceleration at point B is the centripetal acceleration equals to velocity squared divided by the radius.
ac=v2/ r
ac = (6.29)2 / (136.31)
ac=0.29 m/s2
In component form it is given by;
a→c= (-0.29cos350î) + (0.29sin350ĵ)
a→c = -0.24î + 0.17ĵ
2. Determine the car's average speed.
Average speed is given by (total path) / (total time);
v = d/t
v = (214) / (34)
v = 6.29 m/s
Average speed is 6.29 m/s.
3. Determine its average acceleration during the 34.0 sec interval.
Average acceleration is given by aavg = v-ut
= (6.29 m/s) - (i)(34 s) =
aavg = 6.53j^-i^34
aavg = -0.192i^+0.192j^ m/s2

Determine its average acceleration during the 34.0 sec interval.
Average acceleration is given by aavg = v-ut
= (6.29 m/s) - (i)(34 s) =
aavg = 6.53j^-i^34
aavg = -0.192i^+0.192j^ m/s2

Step by step
Solved in 3 steps with 4 images









