d) From these plots, obtain the first harmonics (amplitude and phase) for n = 0,1, 2,3, 4,5. Write a Fourier series expansion in the formx(0) = 4, cos(n@ +9,) e) Take the signal back to the time domain. Write a Fourier series expansion in the form x(1) = £4, cos(no,t+9,)
d) From these plots, obtain the first harmonics (amplitude and phase) for n = 0,1, 2,3, 4,5. Write a Fourier series expansion in the formx(0) = 4, cos(n@ +9,) e) Take the signal back to the time domain. Write a Fourier series expansion in the form x(1) = £4, cos(no,t+9,)
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:Robert L. Boylestad
Chapter1: Introduction
Section: Chapter Questions
Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...
Related questions
Question
I need help with part d and part e. Please show clearly how to solve those parts. Thank you.

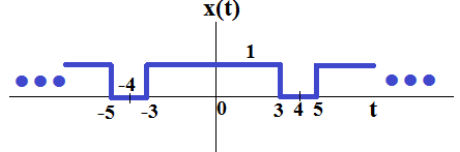
In the graph presented as Figure 1, the signal \( x(t) \) is a piecewise function that alternates between values of 1 and -4 over time \( t \), creating a rectangular waveform pattern. This periodic signal has a series of flat segments between the time marks -5 and 5.
**Objective:**
We wish to obtain the signal harmonics via the Fourier Series.
**Tasks:**
a) Take the signal from the time domain to the \( \theta \) domain.
b) Find an expression for the Fourier coefficients \( c_n \). Use this expression to find \( c_0, c_1, c_2, c_3, c_4, c_5 \) in polar form.
c) Plot \( |c_n| \) and \(\angle c_n\) as a function of \( n \) for \( n = 0, 1, 2, 3, 4, 5 \).
d) From these plots, obtain the first harmonics (amplitude and phase) for \( n = 0, 1, 2, 3, 4, 5 \). Write a Fourier series expansion in the form:
\[
x(\theta) \approx \sum_{n=0}^{5} A_n \cos(n \theta + \phi_n)
\]
e) Take the signal back to the time domain. Write a Fourier series expansion in the form:
\[
x(t) \approx \sum_{n=0}^{5} A_n \cos(n \omega_0 t + \phi_n)
\]
These tasks will assist in deriving the harmonics of the signal \( x(t) \) using Fourier series techniques, converting between time and frequency domains.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ffb9a7c18-65f1-48ed-bb7e-4937a04e4157%2Fc526f029-fa9f-42a8-ac5f-3cc9b8e938a3%2Fxiqviu_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Fourier Series - Exponential Form**
Consider the periodic signal \( x(t) \) depicted in Figure 1.

In the graph presented as Figure 1, the signal \( x(t) \) is a piecewise function that alternates between values of 1 and -4 over time \( t \), creating a rectangular waveform pattern. This periodic signal has a series of flat segments between the time marks -5 and 5.
**Objective:**
We wish to obtain the signal harmonics via the Fourier Series.
**Tasks:**
a) Take the signal from the time domain to the \( \theta \) domain.
b) Find an expression for the Fourier coefficients \( c_n \). Use this expression to find \( c_0, c_1, c_2, c_3, c_4, c_5 \) in polar form.
c) Plot \( |c_n| \) and \(\angle c_n\) as a function of \( n \) for \( n = 0, 1, 2, 3, 4, 5 \).
d) From these plots, obtain the first harmonics (amplitude and phase) for \( n = 0, 1, 2, 3, 4, 5 \). Write a Fourier series expansion in the form:
\[
x(\theta) \approx \sum_{n=0}^{5} A_n \cos(n \theta + \phi_n)
\]
e) Take the signal back to the time domain. Write a Fourier series expansion in the form:
\[
x(t) \approx \sum_{n=0}^{5} A_n \cos(n \omega_0 t + \phi_n)
\]
These tasks will assist in deriving the harmonics of the signal \( x(t) \) using Fourier series techniques, converting between time and frequency domains.
Expert Solution
Step 1
We are given the following periodic signal x(t):
(d) we have to plot and as a function of n & from these plots, we have to obtain the first harmonics (amplitude and phase) for n = 0,1,2,3,4,5. Also, we have to write a Fourier series expansion in the form:
(e) We have to write a Fourier series expansion in the form:
Step by step
Solved in 6 steps with 3 images

Recommended textbooks for you

Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON

Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning

Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education

Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON

Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning

Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education

Fundamentals of Electric Circuits
Electrical Engineering
ISBN:
9780078028229
Author:
Charles K Alexander, Matthew Sadiku
Publisher:
McGraw-Hill Education

Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:
9780134746968
Author:
James W. Nilsson, Susan Riedel
Publisher:
PEARSON

Engineering Electromagnetics
Electrical Engineering
ISBN:
9780078028151
Author:
Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:
Mcgraw-hill Education,