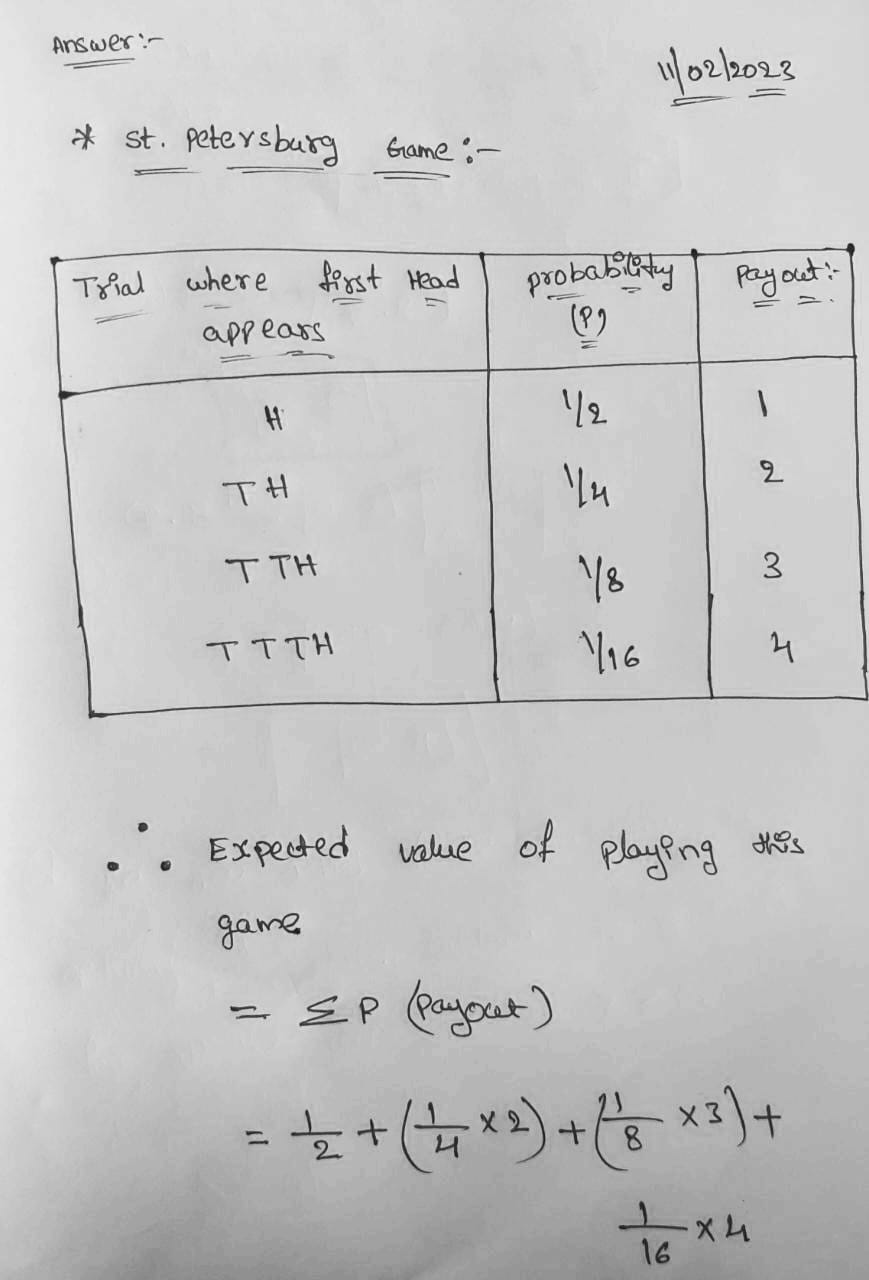
Consider the St. Petersburg Paradox problem first discussed by Daniel Bernoulli in 1738. The game consists of tossing a coin. The player gets a payoff of where n is the number of times the coin is tossed to get the first head. So, if the sequence of tosses yields TTTH, you get a payoff of; this payoff occurs with probability . Compute the expected value of playing this game. (b) Assume that utility U is a function of wealth X given by U = X.5 and that X = $1,000,000. In this part of the question, assume that the game ends
Consider the St. Petersburg Paradox problem first discussed by Daniel Bernoulli in 1738. The game consists of tossing a coin. The player gets a payoff of where n is the number of times the coin is tossed to get the first head. So, if the sequence of tosses yields TTTH, you get a payoff of; this payoff occurs with probability . Compute the
(b) Assume that utility U is a
(c) What is the most you would pay to play the game if you require that your expected utility after playing the game must be at least equal to your utility before playing the game? Suppose you initially contemplate paying $100 to play this game. Use the Goal Seek function (found in Data, What-If Analysis) or Solver (found in Data) in Excel and show your Excel work in the detailed part of your submission.
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images
