Consider a star whose density increases toward its center. If we model this star as a series of concentric shells (each shell having its own uniform density), then the equation of mass continuity relates the mass in each shell to the density and volume of the shell. The star has the following two regimes: Core: ⍴r = ⍴0 from r = 0 to r = r0 Envelope: ⍴r = ⍴0(r/r0)-2 from r = r0 to r = R Integrate the equation of mass continuity (see provided image) over the appropriate ranges to find expressions for the masses in the core and in the envelope. Add the two expressions to find an alegbraic expression for the total M inside R.
Consider a star whose density increases toward its center. If we model this star as a series of concentric shells (each shell having its own uniform density), then the equation of mass continuity relates the mass in each shell to the density and volume of the shell. The star has the following two regimes: Core: ⍴r = ⍴0 from r = 0 to r = r0 Envelope: ⍴r = ⍴0(r/r0)-2 from r = r0 to r = R Integrate the equation of mass continuity (see provided image) over the appropriate ranges to find expressions for the masses in the core and in the envelope. Add the two expressions to find an alegbraic expression for the total M inside R.
Related questions
Question
Consider a star whose density increases toward its center. If we model this star as a series of concentric shells (each shell having its own uniform density), then the equation of mass continuity relates the mass in each shell to the density and volume of the shell. The star has the following two regimes:
- Core: ⍴r = ⍴0 from r = 0 to r = r0
- Envelope: ⍴r = ⍴0(r/r0)-2 from r = r0 to r = R
Integrate the equation of mass continuity (see provided image) over the appropriate ranges to find expressions for the masses in the core and in the envelope. Add the two expressions to find an alegbraic expression for the total M inside R.
![The equation presented is:
\[
\frac{dM(r)}{dr} = 4\pi r^2 \rho(r)
\]
This is a differential equation that often appears in astrophysics, particularly in the context of stellar structure. It describes how the mass \( M(r) \) contained within a sphere of radius \( r \) changes with respect to the radius. Here:
- \( dM(r)/dr \) is the derivative of the mass with respect to the radius, indicating how the mass changes as the radius increases.
- \( 4\pi r^2 \) represents the surface area of a sphere with radius \( r \).
- \( \rho(r) \) is the density as a function of radius.
This equation essentially states that the rate of change of mass with respect to radius is proportional to the surface area at that radius and the density at that point.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Faf4d5de9-a3ed-408a-b8ea-03a65e9854b7%2F0c9556cd-fe04-44d5-a90e-d6c3cbcb2075%2F0d3g9xp_processed.png&w=3840&q=75)
Transcribed Image Text:The equation presented is:
\[
\frac{dM(r)}{dr} = 4\pi r^2 \rho(r)
\]
This is a differential equation that often appears in astrophysics, particularly in the context of stellar structure. It describes how the mass \( M(r) \) contained within a sphere of radius \( r \) changes with respect to the radius. Here:
- \( dM(r)/dr \) is the derivative of the mass with respect to the radius, indicating how the mass changes as the radius increases.
- \( 4\pi r^2 \) represents the surface area of a sphere with radius \( r \).
- \( \rho(r) \) is the density as a function of radius.
This equation essentially states that the rate of change of mass with respect to radius is proportional to the surface area at that radius and the density at that point.
Expert Solution
Step 1
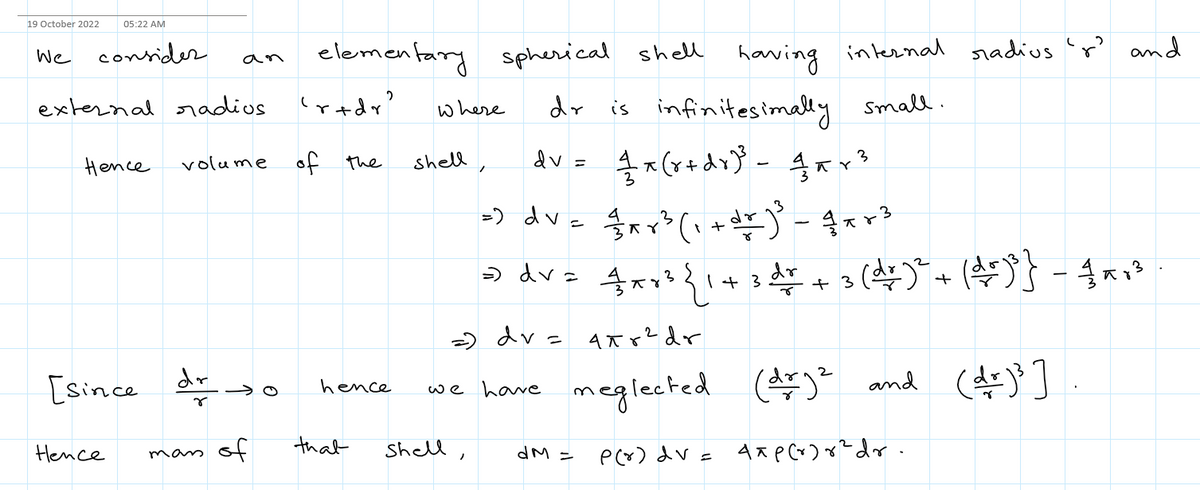
Step by step
Solved in 2 steps with 2 images
