An ecologist wishes to mark off a circular sampling region having radius 12 m. However, the radius of the resulting region is actu random variable R with the following pdf. -far- f(r) = -7)²] - (12- 0 11 ≤ r ≤ 13 otherwise What is the expected area of the resulting circular region? (Round your answer to two decimal places.) * m² Need Help? Read It
An ecologist wishes to mark off a circular sampling region having radius 12 m. However, the radius of the resulting region is actu random variable R with the following pdf. -far- f(r) = -7)²] - (12- 0 11 ≤ r ≤ 13 otherwise What is the expected area of the resulting circular region? (Round your answer to two decimal places.) * m² Need Help? Read It
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
![An ecologist wishes to mark off a circular sampling region having a radius of 12 meters. However, the radius of the resulting region is actually a random variable \( R \) with the following probability density function (pdf):
\[
f(r) =
\begin{cases}
\frac{3}{4} \left[ 1 - (12 - r)^2 \right] & \text{for } 11 \leq r \leq 13 \\
0 & \text{otherwise}
\end{cases}
\]
What is the expected area of the resulting circular region? (Round your answer to two decimal places.)
\[
\boxed{ \hspace{2cm} } \text{ m}^2
\]
**Need Help?** [Read It]
---
**Explanation of the Function:**
This pdf specifies that the probability distribution of the radius \( r \) is valid between 11 and 13 meters, with \( f(r) \) being nonzero only within this range. Outside this range, the probability density is zero. The function \( \frac{3}{4} \left[ 1 - (12 - r)^2 \right] \) defines how the radius varies within this interval.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F4927fb7d-fe4d-496e-94ae-b9c9f1ed73cb%2Fb847ac04-0f87-4c8c-9df5-8569adae6a7e%2Fqb92nws_processed.jpeg&w=3840&q=75)
Transcribed Image Text:An ecologist wishes to mark off a circular sampling region having a radius of 12 meters. However, the radius of the resulting region is actually a random variable \( R \) with the following probability density function (pdf):
\[
f(r) =
\begin{cases}
\frac{3}{4} \left[ 1 - (12 - r)^2 \right] & \text{for } 11 \leq r \leq 13 \\
0 & \text{otherwise}
\end{cases}
\]
What is the expected area of the resulting circular region? (Round your answer to two decimal places.)
\[
\boxed{ \hspace{2cm} } \text{ m}^2
\]
**Need Help?** [Read It]
---
**Explanation of the Function:**
This pdf specifies that the probability distribution of the radius \( r \) is valid between 11 and 13 meters, with \( f(r) \) being nonzero only within this range. Outside this range, the probability density is zero. The function \( \frac{3}{4} \left[ 1 - (12 - r)^2 \right] \) defines how the radius varies within this interval.
Expert Solution
Step 1: Introducing the given information
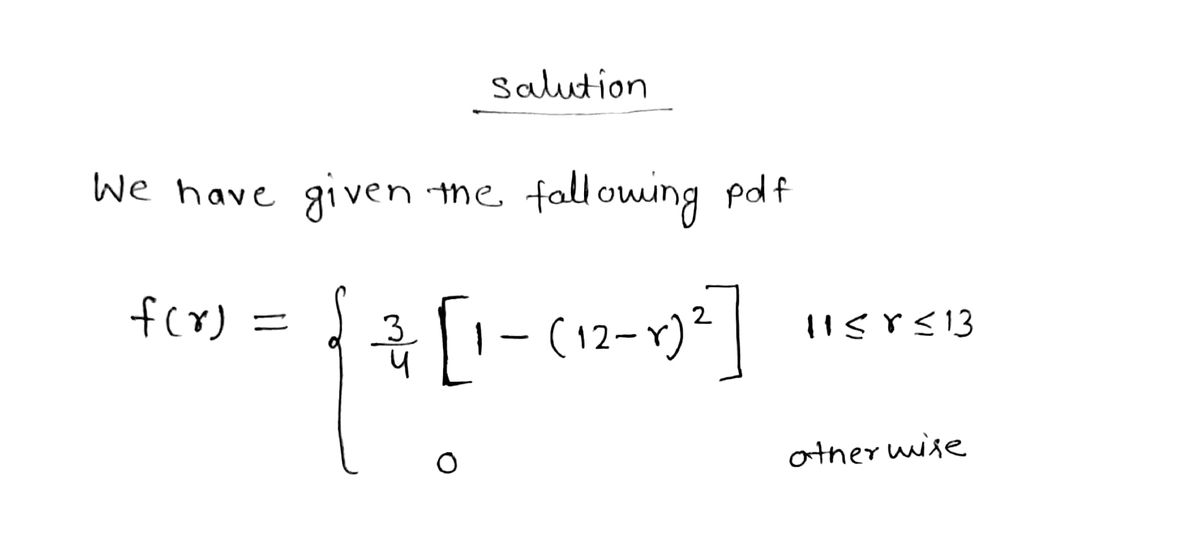
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman