(AA) ²(AB)² ≥ ¹(i[ÂÂ])² If [ÂÂ]=iñ, and  and ☎ represent Hermitian operators corresponding to observable properties, what is the minimum value that AA AB can have? Report your answer as a decimal number with three significant figures.
(AA) ²(AB)² ≥ ¹(i[ÂÂ])² If [ÂÂ]=iñ, and  and ☎ represent Hermitian operators corresponding to observable properties, what is the minimum value that AA AB can have? Report your answer as a decimal number with three significant figures.
Related questions
Question
![(AA) ²( ▲ B) ²≥ ½ (i[ÂÂ])²
If [ÂÂ]=iñ, and  and represent Hermitian operators corresponding to observable properties, what is the minimum
value that AA AB can have?
Report your answer as a decimal number with three significant figures.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fd76a2d57-02e6-4734-ba8a-6fadc8c476a5%2Fe1892210-e84c-4c4f-aafc-99b58a00ed38%2Ffw495hl_processed.png&w=3840&q=75)
Transcribed Image Text:(AA) ²( ▲ B) ²≥ ½ (i[ÂÂ])²
If [ÂÂ]=iñ, and  and represent Hermitian operators corresponding to observable properties, what is the minimum
value that AA AB can have?
Report your answer as a decimal number with three significant figures.
Expert Solution
Step 1
The required solution is following.
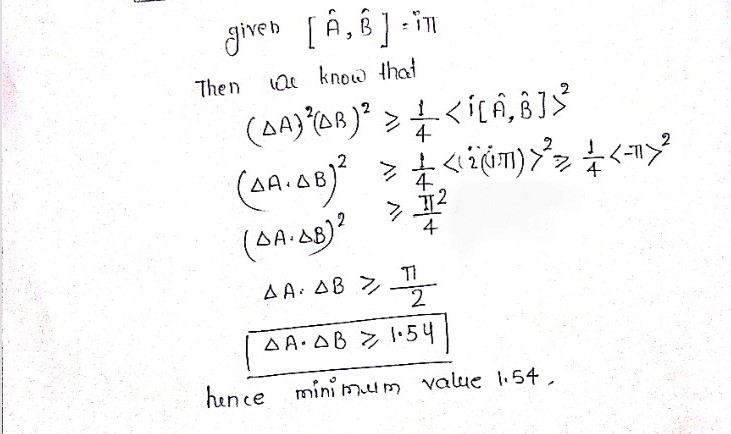
Step by step
Solved in 2 steps with 1 images
