Homework Help is Here – Start Your Trial Now!
Science
Advanced Physics
If then the harmonic is even. If then the harmonic is odd. ПY™(0, 4) = Y(−0, − p) пY™(0, d) = − Y™(0, ¢) -

If then the harmonic is even. If then the harmonic is odd. ПY™(0, 4) = Y(−0, − p) пY™(0, d) = − Y™(0, ¢) -

icon
Related questions
Question

please prove this

• If then the harmonic is even. • If then the harmonic is odd. IIY(0, d) = Y(-0, − p) IIY (0,0) = -Y(0, d) (13) (14)
Transcribed Image Text:• If then the harmonic is even. • If then the harmonic is odd. IIY(0, d) = Y(-0, − p) IIY (0,0) = -Y(0, d) (13) (14)
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 4 steps with 4 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

Bit confused you say with is the definition of a complex conjugate but all I've ever seen is |X|^2=(X*)(X). Can you provide maybe a reference or proof of this?

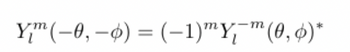
Ym(-0,-) = (-1)"Y(0, 0)*
Transcribed Image Text:Ym(-0,-) = (-1)"Y(0, 0)*
Solution
Bartleby Expert
SEE SOLUTION