(a) The electric potential in a region is given by the equation V(x, y) = (1.00) xyz +2.00V sin (3.00-x). What is the force on a 65.4 mC located at position (3.30 m, 4.21 m,-1.80 m)? Give your answer in vector component notation. .
(a) The electric potential in a region is given by the equation V(x, y) = (1.00) xyz +2.00V sin (3.00-x). What is the force on a 65.4 mC located at position (3.30 m, 4.21 m,-1.80 m)? Give your answer in vector component notation. .
Related questions
Question
![**Problem (a):**
The electric potential in a region is given by the equation:
\[ V(x, y) = \left(1.00 \, \frac{V}{m}\right) xyz + 2.00V \cdot \sin \left(3.00 \, \frac{1}{m} \cdot x \right) \]
You are asked to find the force on a charge of 65.4 mC located at the position (3.30 m, 4.21 m, -1.80 m). Calculate the force in vector component notation.
**Problem (b):**
The electric potential in a region is given by the equation:
\[ V(x, y, z) = \left(2.40 \, \frac{V}{m^3}\right) x^2 y + \left(1.5 \, V\right) e^{(1.00 \, \frac{1}{m^2}) z} \]
You are asked to find the force on a charge of 12.6 mC located at the position (-1.30 m, 2.48 m, -2.10 m). Calculate the force in vector component notation.
**Explanation:**
Both problems involve calculating the force on a charge by determining the electric potential at a given position. Students should apply vector calculus and electrostatic principles to find the components of force acting on the charge located at specific coordinates.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fefc0e927-4815-4e2f-82d9-9b6b5f419d74%2Fa8c61821-3d5d-4c00-9fec-24d9303182d0%2Fglvs2o_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem (a):**
The electric potential in a region is given by the equation:
\[ V(x, y) = \left(1.00 \, \frac{V}{m}\right) xyz + 2.00V \cdot \sin \left(3.00 \, \frac{1}{m} \cdot x \right) \]
You are asked to find the force on a charge of 65.4 mC located at the position (3.30 m, 4.21 m, -1.80 m). Calculate the force in vector component notation.
**Problem (b):**
The electric potential in a region is given by the equation:
\[ V(x, y, z) = \left(2.40 \, \frac{V}{m^3}\right) x^2 y + \left(1.5 \, V\right) e^{(1.00 \, \frac{1}{m^2}) z} \]
You are asked to find the force on a charge of 12.6 mC located at the position (-1.30 m, 2.48 m, -2.10 m). Calculate the force in vector component notation.
**Explanation:**
Both problems involve calculating the force on a charge by determining the electric potential at a given position. Students should apply vector calculus and electrostatic principles to find the components of force acting on the charge located at specific coordinates.
Expert Solution
Step 1
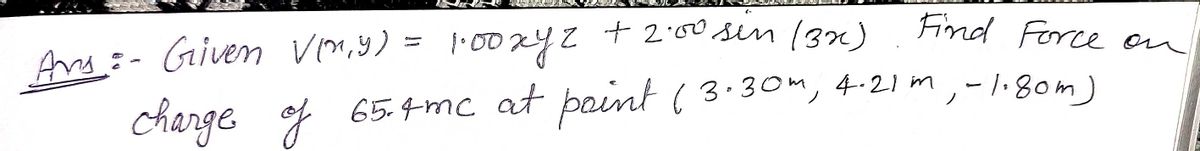
Step by step
Solved in 2 steps with 2 images
