A sunscreen company is attempting to improve upon their formula so that it lasts in water longer. They have 4 lead scientists who each came up with a different formulas. In order to see if there is a difference in the time the sunscreen lasts the CEO collects a random sample of each of the four sunscreens the data is shown below. Test the claim that at least one sunscreen has a different lifespan in water at a 0.10 level of significance. Sunscreen A Sunscreen B Sunscreen C Sunscreen D 66 68 57 73 73 55 65 53 48 45 44 77 52 38 42 62 40 72 62 69 65 32 66 48 The hypotheses for this ANOVA test would be: H0:μA=μB=μC=μDH0:μA=μB=μC=μD HA:HA: At least one mean is different. (claim) α=0.10α=0.10 Complete the ANOVA table below: (round answers to 3 decimal places) SS df MS F p-value Between Within The decision of the test is to: do not reject H0H0 reject H0H0 The final conclusion is: There is enough evidence to reject the claim that at least one sunscreen lasts a different amount of time. There is not enough evidence to support the claim that at least one sunscreen lasts a different amount of time. There is enough evidence to support the claim that at least one sunscreen lasts a different amount of time. There is not enough evidence to reject the claim that at least one sunscreen lasts a different amount of time.

Name: A sunscreen company is attempting to improve upon their formula so tha
Uploaded: 2024-03-20T07:07:12.000Z
Channel: Bartleby
Description: A sunscreen company is attempting to improve upon their formula so that it lasts in water longer. They have 4 lead scientists who each came up with a different formulas. In order to see if there is a difference in the time the sunscreen lasts the CEO

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Topic Video

Question

100%

A sunscreen company is attempting to improve upon their formula so that it lasts in water longer. They have 4 lead scientists who each came up with a different formulas. In order to see if there is a difference in the time the sunscreen lasts the CEO collects a random sample of each of the four sunscreens the data is shown below. Test the claim that at least one sunscreen has a different lifespan in water at a 0.10 level of significance.

Sunscreen A	Sunscreen B	Sunscreen C	Sunscreen D
66	68	57	73
73	55	65	53
48	45	44	77
52	38	42	62
40	72	62	69
65	32	66	48

The hypotheses for this ANOVA test would be:

H0:μA=μB=μC=μDH0:μA=μB=μC=μD

HA:HA: At least one mean is different. (claim)

α=0.10α=0.10

Complete the ANOVA table below: (round answers to 3 decimal places)

	SS	df	MS	F	p-value
Between
Within

The decision of the test is to:

do not reject H0H0
reject H0H0

The final conclusion is:

There is enough evidence to reject the claim that at least one sunscreen lasts a different amount of time.
There is not enough evidence to support the claim that at least one sunscreen lasts a different amount of time.
There is enough evidence to support the claim that at least one sunscreen lasts a different amount of time.
There is not enough evidence to reject the claim that at least one sunscreen lasts a different amount of time.

Expert Solution

Step 1

State the hypotheses:

H₀:μ_A=μ_B=μ_C=μ_D

H_A: At least one mean is different. (claim)

The level of significance is 0.05.

Procedure to obtain One-Way ANOVA using the EXCEL:

Go to Data -> Data Analysis.
Select “Anova: Single Factor” from Analysis Tool.
Select the columns “Sunscreen A”, “Sunscreen B”, “Sunscreen C” and “Sunscreen D” in Input range and click Ok.

Output:

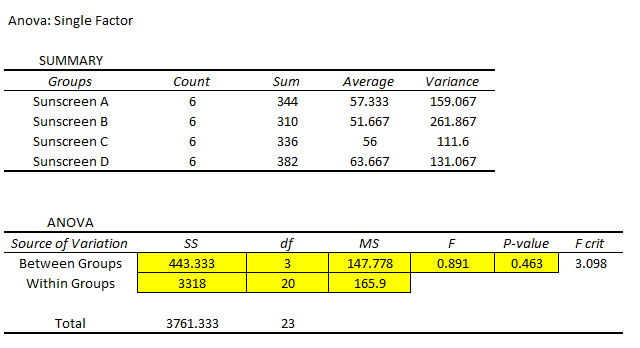
From the output the F-ratio is 0.891.

P-value:

From the output, the P-value is 0.463.

Step by step

Solved in 2 steps with 1 images

Knowledge Booster

$Hypothesis Tests and Confidence Intervals for Means$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions