A square matrix A is idempotent if A² A. Let V be the vector space of all 2 x 2 matrices with real entries. Let H be the set of all 2 x 2 idempotent matrices with real entries. Is H a subspace of the vector space V? 1. Is H nonempty? choose [JE 2. Is H closed under addition? If it is, enter CLOSED. If it is not, enter two matrices in H whose sum is not in H, using a comma separated list and syntax such as [[1,2], [3,4]], [[5,6], [7,8]] for the answer (Hint: to show that H is not closed under addition, it is sufficient to find two idempotent matrices A and B such that (A + B)² (A + B).) 3. Is H closed under scalar multiplication? If it is, enter CLOSED. If it is not, enter a scalar in R and a matrix in H whose product is not in H, using a comma separated list and syntax such as 2, [[3,4], [5,6]] for the answer 2, (Hint: to show that H is not closed under scalar multiplication, it is sufficient to find a real number and an idempotent matrix A such that (rA)² # (rA).) 2, [³6]. 4. Is H a subspace of the vector space V? You should be able to justify your answer by writing a complete, coherent, and detailed proof based on your answers to parts 1-3. choose
A square matrix A is idempotent if A² A. Let V be the vector space of all 2 x 2 matrices with real entries. Let H be the set of all 2 x 2 idempotent matrices with real entries. Is H a subspace of the vector space V? 1. Is H nonempty? choose [JE 2. Is H closed under addition? If it is, enter CLOSED. If it is not, enter two matrices in H whose sum is not in H, using a comma separated list and syntax such as [[1,2], [3,4]], [[5,6], [7,8]] for the answer (Hint: to show that H is not closed under addition, it is sufficient to find two idempotent matrices A and B such that (A + B)² (A + B).) 3. Is H closed under scalar multiplication? If it is, enter CLOSED. If it is not, enter a scalar in R and a matrix in H whose product is not in H, using a comma separated list and syntax such as 2, [[3,4], [5,6]] for the answer 2, (Hint: to show that H is not closed under scalar multiplication, it is sufficient to find a real number and an idempotent matrix A such that (rA)² # (rA).) 2, [³6]. 4. Is H a subspace of the vector space V? You should be able to justify your answer by writing a complete, coherent, and detailed proof based on your answers to parts 1-3. choose
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![A square matrix A is idempotent if A² =
Let V be the vector space of all 2 × 2 matrices with real entries. Let H be the set of all 2 × 2 idempotent matrices with real entries. Is H a subspace of the vector space V?
1. Is H nonempty?
choose
= A.
2. Is H closed under addition? If it is, enter CLOSED. If it is not, enter two matrices in H whose sum is not in H, using a comma separated list and syntax such as [[1,2], [3,4]], [[5,6],[7,8]] for the answer
(Hint: to show that I is not closed under addition, it is sufficient to find two idempotent matrices A and B such that (A + B)² ‡ (A + B).)
2 5
[31].69]
8]
7
[34]
5 6
3. Is H closed under scalar multiplication? If it is, enter CLOSED. If it is not, enter a scalar in R and a matrix in H whose product is not in H, using a comma separated list and syntax such as 2, [[3,4],[5,6]] for the answer 2,
(Hint: to show that H is not closed under scalar multiplication, it is sufficient to find a real number and an idempotent matrix A such that (rA)² ‡ (rA).)
4. Is H a subspace of the vector space V? You should be able to justify your answer by writing a complete, coherent, and detailed proof based on your answers to parts 1-3.
choose
ст со](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F8ff93d80-f747-4f15-803d-56788ff3d116%2F797dba0b-fda7-4ce2-9fd4-354d77a4bcdb%2Fo38oebp_processed.png&w=3840&q=75)
Transcribed Image Text:A square matrix A is idempotent if A² =
Let V be the vector space of all 2 × 2 matrices with real entries. Let H be the set of all 2 × 2 idempotent matrices with real entries. Is H a subspace of the vector space V?
1. Is H nonempty?
choose
= A.
2. Is H closed under addition? If it is, enter CLOSED. If it is not, enter two matrices in H whose sum is not in H, using a comma separated list and syntax such as [[1,2], [3,4]], [[5,6],[7,8]] for the answer
(Hint: to show that I is not closed under addition, it is sufficient to find two idempotent matrices A and B such that (A + B)² ‡ (A + B).)
2 5
[31].69]
8]
7
[34]
5 6
3. Is H closed under scalar multiplication? If it is, enter CLOSED. If it is not, enter a scalar in R and a matrix in H whose product is not in H, using a comma separated list and syntax such as 2, [[3,4],[5,6]] for the answer 2,
(Hint: to show that H is not closed under scalar multiplication, it is sufficient to find a real number and an idempotent matrix A such that (rA)² ‡ (rA).)
4. Is H a subspace of the vector space V? You should be able to justify your answer by writing a complete, coherent, and detailed proof based on your answers to parts 1-3.
choose
ст со
Expert Solution
Step 1: Solve 1
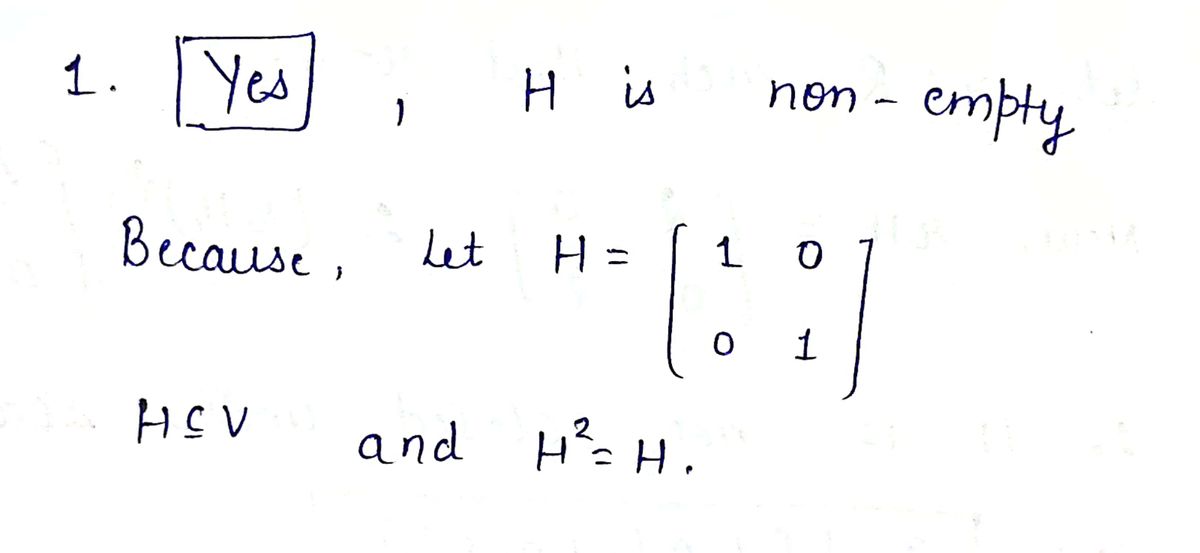
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

