A random sample of 360 married couples found that 284 had two or more personality preferences in common. In another random sample of 568 married couples, it was found that only 36 had no preferences in common. Let p1 be the population proportion of all married couples who have two or more personality preferences in common. Let p2 be the population proportion of all married couples who have no personality preferences in common. (a) Find a 90% confidence interval for p1 – p2. (Use 3 decimal places.) lower limit = upper limit = (b) Explain the meaning of the confidence interval in part (a) in the context of this problem. Does the confidence interval contain all positive, all negative, or both positive and negative numbers? What does this tell you (at the 90% confidence level) about the proportion of married couples with two or more personality preferences in common compared with the proportion of married couples sharing no personality preferences in common? Choose one: -We can not make any conclusions using this confidence interval. -Because the interval contains both positive and negative numbers, we can not say that a higher proportion of married couples have two or more personality preferences in common. -Because the interval contains only positive numbers, we can say that a higher proportion of married couples have two or more personality preferences in common. -Because the interval contains only negative numbers, we can say that a higher proportion of married couples have no personality preferences in common.
A random sample of 360 married couples found that 284 had two or more personality preferences in common. In another random sample of 568 married couples, it was found that only 36 had no preferences in common. Let p1 be the population proportion of all married couples who have two or more personality preferences in common. Let p2 be the population proportion of all married couples who have no personality preferences in common.
(a) Find a 90% confidence interval for p1 – p2. (Use 3 decimal places.)
lower limit =
upper limit =
(b) Explain the meaning of the confidence interval in part (a) in the context of this problem. Does the confidence interval contain all positive, all negative, or both positive and negative numbers? What does this tell you (at the 90% confidence level) about the proportion of married couples with two or more personality preferences in common compared with the proportion of married couples sharing no personality preferences in common? Choose one:
-We can not make any conclusions using this confidence interval.
-Because the interval contains both positive and negative numbers, we can not say that a higher proportion of married couples have two or more personality preferences in common.
-Because the interval contains only positive numbers, we can say that a higher proportion of married couples have two or more personality preferences in common.
-Because the interval contains only negative numbers, we can say that a higher proportion of married couples have no personality preferences in common.
From the provided information,
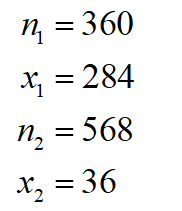
Step by step
Solved in 4 steps with 3 images









