A nursing school professor is interested in determining how her college students compare to the national average when it comes to the Final Practicum Exam. The exam has a µ = 100 and σ = 20. There has been no evidence to suggest whether those seniors score better or worse than the national average and she is curious as to how her class (N=17) compares. Female Class Bench Ability (lbs.) 1 130 2 100 3 99 4 114 5 130 6 97 7 114 8 135 9 128 10 128 11 116 12 141 13 113 14 116 Write the null and alternative hypothesis in statistical form: Determine the mean for the sample: Apply the z-test formula What is your alpha level set to? α Determine the critical value(s) (Zcrit) Label the critical value(s) and indicate the position of the Zobt on the distribution Write the z result in the correct form:
A nursing school professor is interested in determining how her college students compare to the national average when it comes to the Final Practicum Exam. The exam has a µ = 100 and σ = 20. There has been no evidence to suggest whether those seniors score better or worse than the national average and she is curious as to how her class (N=17) compares.
Female Class Bench Ability (lbs.)
|
1 |
130 |
|
2 |
100 |
|
3 |
99 |
|
4 |
114 |
|
5 |
130 |
|
6 |
97 |
|
7 |
114 |
|
8 |
135 |
|
9 |
128 |
|
10 |
128 |
|
11 |
116 |
|
12 |
141 |
|
13 |
113 |
|
14 |
116 |
Write the null and alternative hypothesis in statistical form:
Determine the
Apply the z-test formula
What is your alpha level set to? α
Determine the critical value(s) (Zcrit)
Label the critical value(s) and indicate the position of the Zobt on the distribution
Write the z result in the correct form:
- Given Information :
A nursing school professor is interested in determining how her college students compare to the national average when it comes to the Final Practicum Exam. The exam has a µ = 100 and σ = 20. There has been no evidence to suggest whether those seniors score better or worse than the national average and she is curious as to how her class (N=17) compares.
First, calculate the mean for the given data.
The mean of a data set is commonly known as the average. You find the mean by taking the sum of all the data values and dividing that sum by the total number of data values.
The formula for the mean of a sample is
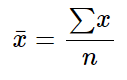
Both of these formulas use the same mathematical process: find the sum of the data values and divide by the total. For the data values entered above, the solution is:
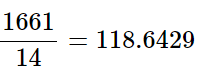
Sample mean = 118.6429
Step by step
Solved in 2 steps with 2 images









