A ife insurence selesmen sells on the avercye policies per week. Use Pai ssun's lqu to cal culate the probebility that n the next 1.5weeks he will Jome policies 2 or policies more policies bett less than 5 M)) assuming that there are probability that in a qiven cley he will sell on e S wiking days per week, what is the policy?


Note:
Hey there! Thank you for the question. As you have posted two different questions, according to our policy, we have solved the first one for you. Please re-post the second one separately.
i.
The number of life insurance policies sold in 1 week, on an average, is 2.
As a result, the number of life insurance policies sold in 1.5 weeks, on an average, is 3 (= 2 × 1.5).
Denote X as the number of life insurance policies sold in a randomly chosen 1.5-week period. It is given that X has a Poisson distribution.
If X ~ Poisson (λ), where λ is the average rate of occurrence of the event of interest in a specified period, where the occurrences are independent of each other, then the probability mass function of X is:
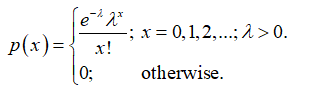
In this, case, it can be said that X has a Poisson distribution with parameter, λ = 3.
It is required to find the probability that the salesman sells some, say X = x policies in a particular 1.5-week period.
Hence, using the probability mass function of a Poisson distribution, the probability that the salesman sells some policies in 1.5 weeks:
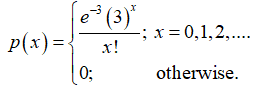
Step by step
Solved in 4 steps with 5 images









