Please walk me through this problem A ball is struck from a height (1.80 m) with an initial velocity of 12.0 m/s at anangle of 42.0° above the horizontal. The ball passes through the center of ahoop before returning to the ground which is 1.80 m below the startingpoint. If the ball is moving horizontally when it goes through the hoop, (hint:make sure you know the condition of equations you want to use.)use g=9.81m/s²1. how long does it take to reach the hoop?2. And how high above the ground is the center of the hoop?3. How far is the ball measured horizontally from the person to where itlanded?40.0°2.00m

Name: Please walk me through this problem A ball is struck from a height (1.
Uploaded: 2024-03-20T06:56:46.000Z
Channel: Bartleby
Description: Please walk me through this problem A ball is struck from a height (1.80 m) with an initial velocity of 12.0 m/s at anangle of 42.0° above the horizontal. The ball passes through the center of ahoop before returning to the ground which is 1.80 m belo

Answered: A ball is struck from a height (1.80 m)…

College Physics

11th Edition

ISBN:9781305952300

Author:Raymond A. Serway, Chris Vuille

Publisher:Raymond A. Serway, Chris Vuille

Chapter1: Units, Trigonometry. And Vectors

Section: Chapter Questions

Problem 1CQ: Estimate the order of magnitude of the length, in meters, of each of the following; (a) a mouse, (b)...

See similar textbooks

Related questions

Concept explainers

Topic Video

Question

100%

Please walk me through this problem

A ball is struck from a height (1.80 m) with an initial velocity of 12.0 m/s at an
angle of 42.0° above the horizontal. The ball passes through the center of a
hoop before returning to the ground which is 1.80 m below the starting
point. If the ball is moving horizontally when it goes through the hoop, (hint:
make sure you know the condition of equations you want to use.)
use g=9.81m/s²
1. how long does it take to reach the hoop?
2. And how high above the ground is the center of the hoop?
3. How far is the ball measured horizontally from the person to where it
landed?
40.0°
2.00
m

Expert Solution

Step 1

When an object is thrown obliquely near the Earth's surface it moves in a curved path. The object is called as projectile and its motion is called as projectile motion. The acceleration of the object is nearly equal to the acceleration due to gravity, g.

Kinematic equations of motion are-

$1) v = u + at 2) s = ut + \frac{1}{2} {at}^{2} 3) v^{2} = u^{2} + 2 as$

where,
$u is initial velocity v is final velocity s is displacement t is time a is acceleration$

Step 2

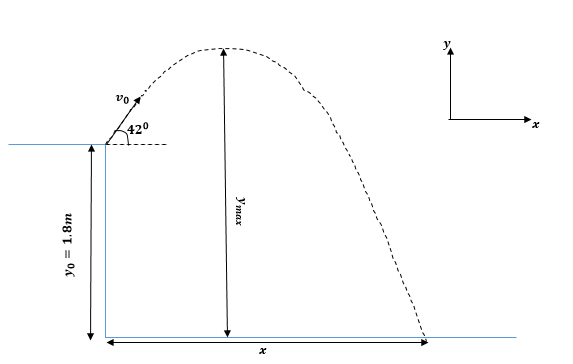
Consider downward motion as negative and upward as positive.

(1)

Since the ball is travelling horizontally at the center of the hoop, so the center of the hoop is the top most point in the motion of ball.

At this point the vertical component of velocity of ball is zero.

Now, apply kinematic equation of motion in vertical direction between the point of launch and the center of the hoop-

$\begin{array}{rcl} \Rightarrow & v_{y} = u_{y} - gt \\ \Rightarrow & 0 = v_{0} \sin (θ) - gt \\ \Rightarrow & t = \frac{12 \times \sin (42)}{9.81} \\ \Rightarrow & t = 0.818 s \end{array}$

where,
$v_{y} is vertical component of final velocity at top most point u_{y} is vertical component of initial velocity$

(2)

Height of the center of hoop from the point of launch of ball is-

$\begin{array}{rcl} \Rightarrow & s = u_{y} t - \frac{1}{2} {gt}^{2} \\ \Rightarrow & s = v_{0} \sin (θ) t - \frac{1}{2} {gt}^{2} \end{array}$
$\begin{array}{rcl} \Rightarrow & s = (12 \sin (42) \times 0.818) - \frac{1}{2} (9.81) {(0.818)}^{2} \end{array}$
$\begin{array}{rcl} \Rightarrow & s = 3.28 m \end{array}$

Therefore, height of center of loop from the ground is given by-

$\begin{array}{rcl} \Rightarrow & y_{\max} = y_{0} + s \\ = & 1.8 + 3.28 \\ = & 5.08 m \end{array}$

(3)

Apply kinematic equation of motion in vertical direction between point of launch and the floor.

$\Rightarrow y = y_{0} + u_{y} t' + \frac{1}{2} gt'^{2} \Rightarrow y = y_{0} + v_{0} \sin (θ) t' + \frac{1}{2} gt'^{2} \Rightarrow \frac{1}{2} (9.81) t'^{2} + 12 \sin (42) t' - 1.8 = 0$

Solving this quadratic equation using quadratic formula-

$\Rightarrow t' = \frac{- 12 \sin (42) \pm \sqrt{{(12 \sin (42))}^{2} - 4 (\frac{9.81}{2}) (- 1.8)}}{2 \times \frac{9.81}{2}} \Rightarrow t' = 0.199 s$

Now,
Horizontal distance moved by ball in time $t'$ is equal to-

$x = v_{0} \cos (42) \times t' x = 12 \cos (42) \times 0.199 x = 1.77 m$

Step by step

Solved in 3 steps with 1 images

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.

Similar questions