5. Given graph of the 4th degree function. a) Identify zeros b) Write a formula for a possible polynomial function that the graph represents using c as the constant factor. c) Use the y-intercept of the function to find c. d) Write the function in standard form. 10 0
5. Given graph of the 4th degree function. a) Identify zeros b) Write a formula for a possible polynomial function that the graph represents using c as the constant factor. c) Use the y-intercept of the function to find c. d) Write the function in standard form. 10 0
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter3: Functions And Graphs
Section3.5: Graphs Of Functions
Problem 34E
Related questions
Question
Transcribed Image Text:5. Given graph of the 4th degree function.
a) Identify zeros
b) Write a formula for a possible polynomial
function that the graph represents using c as
the constant factor.
c) Use the y-intercept of the function to find c.
d) Write the function in standard form.
10
0
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
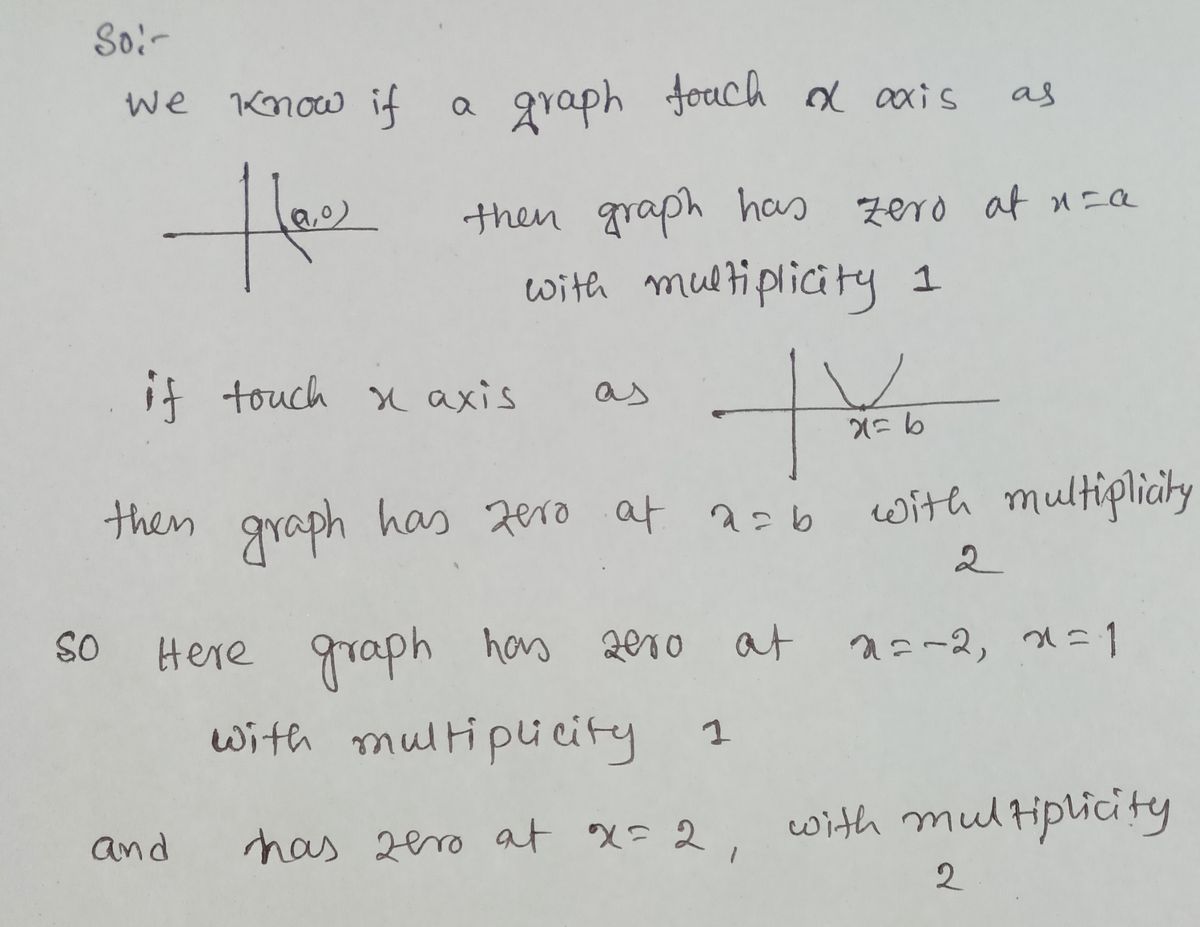
Step by step
Solved in 3 steps with 3 images
Recommended textbooks for you
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
Big Ideas Math A Bridge To Success Algebra 1: Stu…
Algebra
ISBN:
9781680331141
Author:
HOUGHTON MIFFLIN HARCOURT
Publisher:
Houghton Mifflin Harcourt
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
Big Ideas Math A Bridge To Success Algebra 1: Stu…
Algebra
ISBN:
9781680331141
Author:
HOUGHTON MIFFLIN HARCOURT
Publisher:
Houghton Mifflin Harcourt
College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning
College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning