4. Use the Gauss law to calculate the magnitude of the electric field from scratch. For the closed surface of integration (the "Gaussian box"), use a shape with two faces, the "caps," parallel and side or sides perpendicular to the charged sheets. Explain all the assumptions you have to make for the electric field and back them up with symmetry arguments. (a) Make a clear sketch of the system and your Gaussian box, including representative area vectors dA and electric field vectors. (b) Calculate the flux integral ƒE•dA. Include an explanation of your reasoning. (c) Calculate Qenc. Include an explanation of your reasoning. (d) Use the Gauss law to calculate the magnitude of the electric field at any point in space.
4. Use the Gauss law to calculate the magnitude of the electric field from scratch. For the closed surface of integration (the "Gaussian box"), use a shape with two faces, the "caps," parallel and side or sides perpendicular to the charged sheets. Explain all the assumptions you have to make for the electric field and back them up with symmetry arguments. (a) Make a clear sketch of the system and your Gaussian box, including representative area vectors dA and electric field vectors. (b) Calculate the flux integral ƒE•dA. Include an explanation of your reasoning. (c) Calculate Qenc. Include an explanation of your reasoning. (d) Use the Gauss law to calculate the magnitude of the electric field at any point in space.
Related questions
Question

Transcribed Image Text:4. Use Gauss's law to calculate the magnitude of the electric field from scratch. For the closed surface of integration (the “Gaussian box”), use a shape with two faces, the “caps,” parallel and side or sides perpendicular to the charged sheets. Explain all the assumptions you have to make for the electric field and back them up with symmetry arguments.
(a) Make a clear sketch of the system and your Gaussian box, including representative area vectors \(dA\) and electric field vectors.
(b) Calculate the flux integral \(\oint \mathbf{E} \cdot d\mathbf{A}\). Include an explanation of your reasoning.
(c) Calculate \(Q_{enc}\). Include an explanation of your reasoning.
(d) Use Gauss's law to calculate the magnitude of the electric field at any point in space.
Expert Solution
Step 1
Suppose we have a uniformly positive charged sheet with charge density σ. Then we have to form a Gaussian surface having shape symmetric to the charge distribution. So let's draw the diagram:
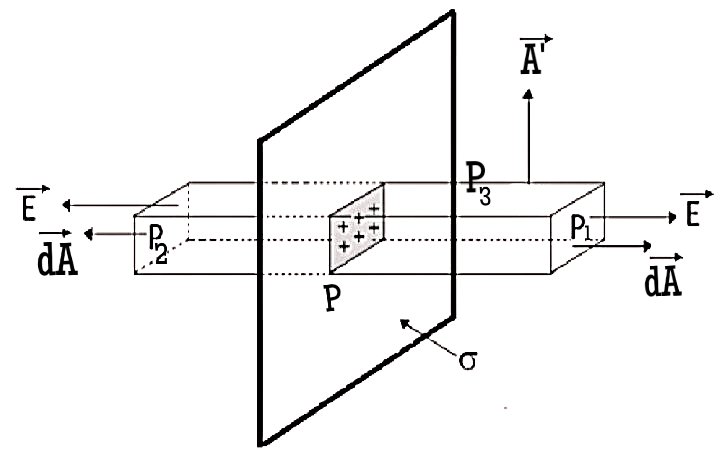
Here the Gaussian surface has three sections of surface one at P1 second at P2 and third between the two i.e. P3.
Step by step
Solved in 4 steps with 8 images
