Homework Help is Here – Start Your Trial Now!
Engineering
Electrical Engineering
3. Calculate the following integral [you have to show your manual calculations leading to the answer although you are allowed to use a math tool to check your answer): S6(2t-5) Pei +2t +3 dt

3. Calculate the following integral [you have to show your manual calculations leading to the answer although you are allowed to use a math tool to check your answer): S6(2t-5) Pei +2t +3 dt

Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:Robert L. Boylestad
Chapter1: Introduction
Section: Chapter Questions
Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...
See similar textbooks
icon
Related questions
Question
Certainly! Here is the transcription of the image for an educational website: --- **Problem 3.** **Calculate the following integral [you have to show your manual calculations leading to the answer although you are allowed to use a math tool to check your answer]:** \[ \int_{-\infty}^{\infty} \delta(2t - 5) \left( t^2 e^{-\frac{t+5}{2}} + 2t + 3 \right) \, dt \] --- **Explanation:** This is an integral involving the Dirac delta function, \(\delta(2t - 5)\), and the expression \(t^2 e^{-\frac{t+5}{2}} + 2t + 3\). The Dirac delta function is a special mathematical function that is very useful in various fields, particularly in physics and engineering, because it “picks out” the value of another function at a specific point. - **Dirac Delta Function:** \(\delta(2t - 5)\) implies that the integral will evaluate the expression only at the point where \(2t - 5 = 0\), which simplifies to \(t = \frac{5}{2}\). - **Expression within the integral:** The expression inside the integral is \(t^2 e^{-\frac{t+5}{2}} + 2t + 3\), and it will be evaluated at \(t = \frac{5}{2}\). - **Calculation Step:** Substitute \(t = \frac{5}{2}\) into the expression: \[ \left( \left(\frac{5}{2}\right)^2 e^{-\frac{\frac{5}{2}+5}{2}} + 2\left(\frac{5}{2}\right) + 3 \right) \] This simplification and evaluation are critical in understanding the behavior of the integral with the delta function. ---
Transcribed Image Text:Certainly! Here is the transcription of the image for an educational website: --- **Problem 3.** **Calculate the following integral [you have to show your manual calculations leading to the answer although you are allowed to use a math tool to check your answer]:** \[ \int_{-\infty}^{\infty} \delta(2t - 5) \left( t^2 e^{-\frac{t+5}{2}} + 2t + 3 \right) \, dt \] --- **Explanation:** This is an integral involving the Dirac delta function, \(\delta(2t - 5)\), and the expression \(t^2 e^{-\frac{t+5}{2}} + 2t + 3\). The Dirac delta function is a special mathematical function that is very useful in various fields, particularly in physics and engineering, because it “picks out” the value of another function at a specific point. - **Dirac Delta Function:** \(\delta(2t - 5)\) implies that the integral will evaluate the expression only at the point where \(2t - 5 = 0\), which simplifies to \(t = \frac{5}{2}\). - **Expression within the integral:** The expression inside the integral is \(t^2 e^{-\frac{t+5}{2}} + 2t + 3\), and it will be evaluated at \(t = \frac{5}{2}\). - **Calculation Step:** Substitute \(t = \frac{5}{2}\) into the expression: \[ \left( \left(\frac{5}{2}\right)^2 e^{-\frac{\frac{5}{2}+5}{2}} + 2\left(\frac{5}{2}\right) + 3 \right) \] This simplification and evaluation are critical in understanding the behavior of the integral with the delta function. ---
Expert Solution
Step 1

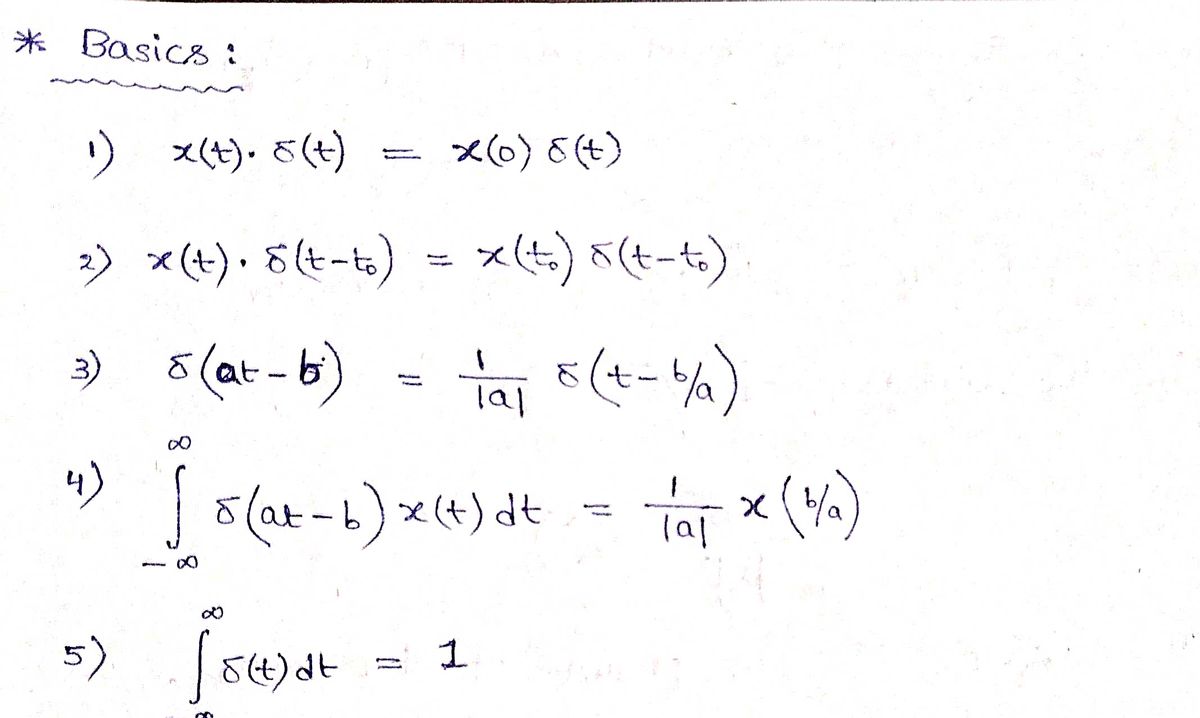
Electrical Engineering homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON
Delmar's Standard Textbook Of Electricity
Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning
Programmable Logic Controllers
Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education
Fundamentals of Electric Circuits
Fundamentals of Electric Circuits
Electrical Engineering
ISBN:
9780078028229
Author:
Charles K Alexander, Matthew Sadiku
Publisher:
McGraw-Hill Education
Electric Circuits. (11th Edition)
Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:
9780134746968
Author:
James W. Nilsson, Susan Riedel
Publisher:
PEARSON
Engineering Electromagnetics
Engineering Electromagnetics
Electrical Engineering
ISBN:
9780078028151
Author:
Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:
Mcgraw-hill Education,
SEE MORE TEXTBOOKS