Homework Help is Here – Start Your Trial Now!
Engineering
Electrical Engineering
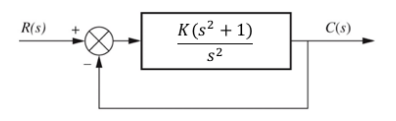
Problem #2 Sketch the root locus for the following system. R(s) K(s² + 1) s² C(s)

Problem #2 Sketch the root locus for the following system. R(s) K(s² + 1) s² C(s)

Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:Robert L. Boylestad
Chapter1: Introduction
Section: Chapter Questions
Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...
See similar textbooks
icon
Related questions
Question

Please answer in typing format please ASAP

Please I will like it please ASAP for

Please answer all subpart either

 

**Problem #2** Sketch the root locus for the following system. **Block Diagram Explanation:** The system depicted is a feedback control system which includes a summation block and a transfer function block. - **Summation Block:** - Inputs: \( R(s) \) and the feedback signal (negative feedback). - Output: The difference (error signal) between \( R(s) \) and the feedback. - **Transfer Function Block:** - Forward Path Transfer Function: \(\frac{K(s^2 + 1)}{s^2}\) - This represents a second-order system with a gain \( K \), a zero at \( s = -1 \), and poles at the origin \( s = 0 \). - **Feedback Path:** - Negative feedback loop from the output \( C(s) \) back to the summation block. **Objective:** - Sketching the root locus requires determining how the poles of the system transfer function change with varying gain \( K \). For educational purposes, a root locus plot would show the path of the closed-loop poles on the complex plane as the gain \( K \) varies from 0 to infinity.
Transcribed Image Text:**Problem #2** Sketch the root locus for the following system. **Block Diagram Explanation:** The system depicted is a feedback control system which includes a summation block and a transfer function block. - **Summation Block:** - Inputs: \( R(s) \) and the feedback signal (negative feedback). - Output: The difference (error signal) between \( R(s) \) and the feedback. - **Transfer Function Block:** - Forward Path Transfer Function: \(\frac{K(s^2 + 1)}{s^2}\) - This represents a second-order system with a gain \( K \), a zero at \( s = -1 \), and poles at the origin \( s = 0 \). - **Feedback Path:** - Negative feedback loop from the output \( C(s) \) back to the summation block. **Objective:** - Sketching the root locus requires determining how the poles of the system transfer function change with varying gain \( K \). For educational purposes, a root locus plot would show the path of the closed-loop poles on the complex plane as the gain \( K \) varies from 0 to infinity.
Expert Solution
Step 1: what is given and what to do:

Given:

a control system,

Electrical Engineering homework question answer, step 1, image 1

To do:

we need to sketch the root locus. 


trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 3 steps with 5 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Knowledge Booster
Root Locus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, electrical-engineering and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON
Delmar's Standard Textbook Of Electricity
Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning
Programmable Logic Controllers
Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education
Fundamentals of Electric Circuits
Fundamentals of Electric Circuits
Electrical Engineering
ISBN:
9780078028229
Author:
Charles K Alexander, Matthew Sadiku
Publisher:
McGraw-Hill Education
Electric Circuits. (11th Edition)
Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:
9780134746968
Author:
James W. Nilsson, Susan Riedel
Publisher:
PEARSON
Engineering Electromagnetics
Engineering Electromagnetics
Electrical Engineering
ISBN:
9780078028151
Author:
Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:
Mcgraw-hill Education,
SEE MORE TEXTBOOKS