Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
2. (a) Let A be a square matrix of order tv 11 with the corresponding and V = Find exponential solutions (t) = = equations x'' = AX.

2. (a) Let A be a square matrix of order tv 11 with the corresponding and V = Find exponential solutions (t) = = equations x'' = AX.

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
2. (a) Let **A** be a square matrix of order two which has eigenvectors \(\vec{u} = \begin{bmatrix} 2 \\ 3 \end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} 4 \\ 1 \end{bmatrix}\) with corresponding eigenvalues \(\lambda = 2\) and \(\lambda = -5\). Find exponential solutions \(\vec{X}(t) = \begin{bmatrix} x_1(t) \\ x_2(t) \end{bmatrix}\) of the system of differential equations \(\vec{X}' = \mathbf{A} \vec{X}\). (b) How do \(x_1(t)\) and \(x_2(t)\) behave in the found solutions as \(t \to \infty\)?
Transcribed Image Text:2. (a) Let **A** be a square matrix of order two which has eigenvectors \(\vec{u} = \begin{bmatrix} 2 \\ 3 \end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} 4 \\ 1 \end{bmatrix}\) with corresponding eigenvalues \(\lambda = 2\) and \(\lambda = -5\). Find exponential solutions \(\vec{X}(t) = \begin{bmatrix} x_1(t) \\ x_2(t) \end{bmatrix}\) of the system of differential equations \(\vec{X}' = \mathbf{A} \vec{X}\). (b) How do \(x_1(t)\) and \(x_2(t)\) behave in the found solutions as \(t \to \infty\)?
Expert Solution
Step 1

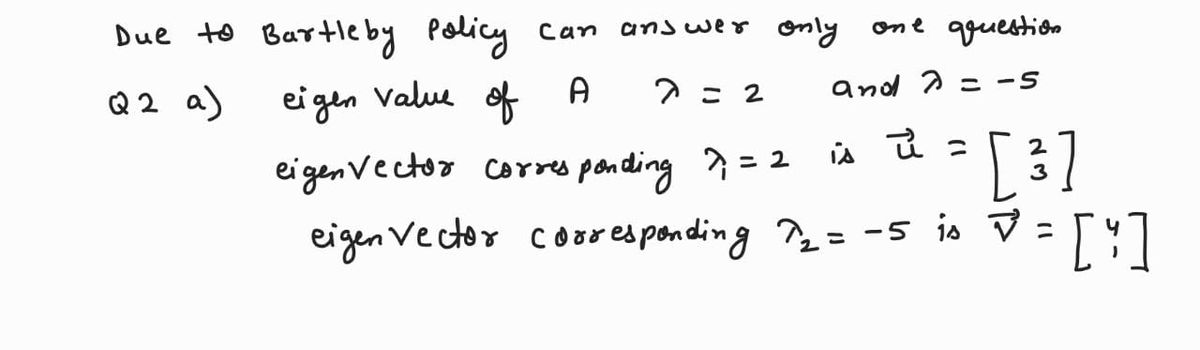
Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS