1. Returning to our old favorite, an infinite square potential is defined by I<0: U (x) = ∞ 0 < x < L: U (x) = 0 r > L: U (x) = ∞ As we've shown, the normalized eigenstates for this systems are /2 tin (7) = Vžsin (Fnz) Show explicitly that the states are orthogonal; that is | (x) vn (x) dx = ôn,m (Hint: You already know this is equal to 1 when n = m. For the case where n m, use standard trig identities to turn the product of sines into cosines of the sum and difference of the arguments.)
1. Returning to our old favorite, an infinite square potential is defined by I<0: U (x) = ∞ 0 < x < L: U (x) = 0 r > L: U (x) = ∞ As we've shown, the normalized eigenstates for this systems are /2 tin (7) = Vžsin (Fnz) Show explicitly that the states are orthogonal; that is | (x) vn (x) dx = ôn,m (Hint: You already know this is equal to 1 when n = m. For the case where n m, use standard trig identities to turn the product of sines into cosines of the sum and difference of the arguments.)
Related questions
Question
help with modern physics question

Transcribed Image Text:1. Returning to our old favorite, an infinite square potential is defined by
I<0: U (x) = ∞
0 < x < L: U (x) = 0
r > L: U (x) = ∞
As we've shown, the normalized eigenstates for this systems are
/2
tin (7) = Vžsin (Fnz)
Show explicitly that the states are orthogonal; that is
| (x) vn (x) dx = ôn,m
(Hint: You already know this is equal to 1 when n = m. For the case where n m, use
standard trig identities to turn the product of sines into cosines of the sum and difference of
the arguments.)
Expert Solution
Step 1
Given wave function in region 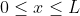
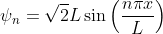
Else it is zero.
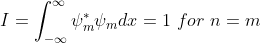
Step by step
Solved in 2 steps with 4 images
