What is meant by graph?

A graph is a non-linear data structure made up of two components namely, vertices and edges. It is represented by as:

G = (V,E)

A graph (G) is a data structure that contains a finite set with ordered pairs called edge (E) and a set of vertices (V). V is a set, whose elements are called nodes, points, or vertices. E is the set of ordered pairs of vertices, called direct edges, arcs, directed lines, or arrows.

Example: In the graph, each user of Facebook is represented as a node (or vertex), where each node is a structure that contains the data such as name, gender, date of birth, id, etc. The nodes are connected to each other via an edge if one user is a friend of another user on Facebook.

Terminology

• Graph is represented by G(V,E) and that is defined by a set of vertices (V) and a set of edges (E).
• Vertex is an individual data element of a graph. It is also known as node.
• Edge is a connecting link between two vertices. Edge is also known as Arc. An edge is represented as a pair of starting vertex and ending vertex.
• Degree d(v) of a vertex is the total number of edges connected to the vertex.

Types of graphs

Graphs are classified into various types namely:

Directed graph

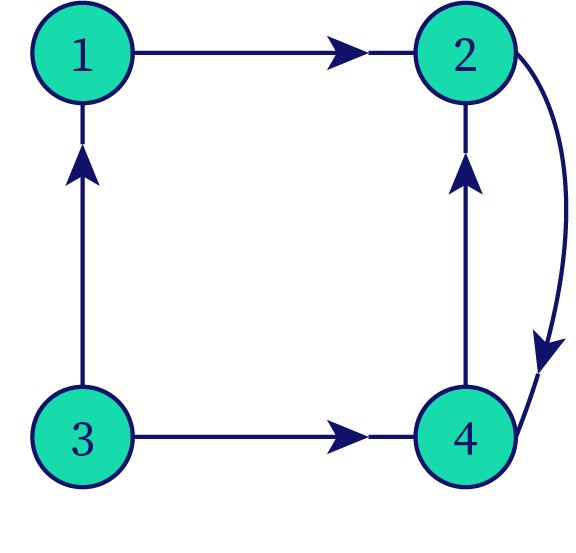
A directed graph is a graph where the edges connect the node in a particular direction. Each edge of the directed graph is uni-directional.

Example: In the below diagram, the graph can be traversed from vertex 1 to 2, 3 to 1, 3 to 4, 4 to 2, and 2 to 4 but not from vertex 2 to 1, 1 to 3, and 4 to 3.

Undirected graph

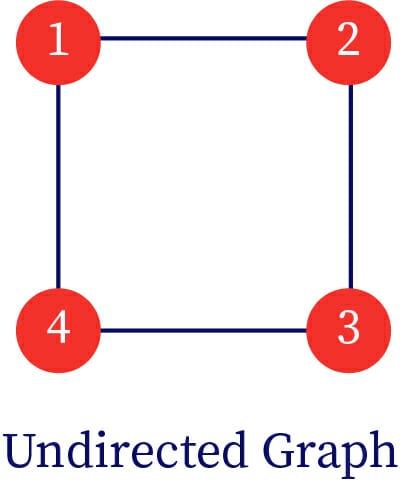
An undirected graph is a type of graph that has all the edges in a bi-directional fashion which means that edges point freely and they do not have any specific direction. 

Example: In the below diagram, the graph can be traversed from node 1 to 2, 2 to 3, 3 to 4, 4 to 1 as well as from node 2 to 1, 3 to 2, 4 to 3, and 1 to 4.

Weighted graph

Every edge in the graph is assigned with weight or cost. A weighted graph can be directed or undirected.

Cyclic

When a graph contains a closed path, then the graph is known as cyclic. A closed path starts and ends at the same vertex. A graph with no cycle is called an acyclic graph.

Tree

A tree is an undirected graph in which two vertices are connected by one path. A tree is an acyclic graph and contains N - 1 edges (N is the number of vertices). Each node in a graph can have multiple parent nodes. Each node (except the root node) comprises exactly one parent node.

Graph representation

Graphs are represented using any one of the following data structures.

Adjacency matrix

An adjacency matrix can be defined as a V*V elements of binary matrix A. The element $A_{i,j}$ is 1, only if their is an edge between the vertices i and j, otherwise it will be 0. The binary matrix might have either 1 or 0 as their value.

The adjacency matrix can be changed for the weighted graph, which stores the weight or cost of the edge instead of storing 0 or 1 in $A_{i,j}$. In an undirected graph, $if A_{i,j} = 1, then A_{j.i} = 1$ and in a directed graph, $if A_{i,j} = 1, then A_{j,i} may or may not be 1.$ The adjacency matrix provides constant-time access (O(1)) to determine if there is an edge between two nodes. The space complexity is $O\left(V^2\right).$

Advantages

• Simple to add an edge in the graph in constant time.
• Easy to determine whether two nodes are adjacent to each other.

Disadvantages

• Requires large memory to store graph.
• Traversing the graph using BFS/DPS algorithms requires $O\left(V^2\right)$ time.

Adjacency list

An adjacency list is a method to represent the graph. It is an array A of lists, where each element in the array A_i is a list that consists of the vertices which are adjacent to vertex i.

In a weighted graph, the edge cost or edge weight is stored with the node/vertex in the list. In an undirected graph, when the list $A_i$ contains vertex j, then vertex i is also stored in the list $A_j$. The adjacency list representation consists of V elements in the array where each element has a list of vertices which depends on the edges connected to that vertex. Thus, storing the vertices takes O(V) space and the elements in each list take O(E) space, so the space complexity is O(V+E).

Advantages

• Simple to retrieve the adjacent nodes of a given node.
• Requires less memory space.
• Simple to check whether a node has edges starting from it.

Disadvantages

• Quite complex to check whether there is an edge between a given pair of nodes.

Graph traversal

The graph traversal is a method to determine the order of node arrangement. The two different graph traversal techniques are:

Depth First Search (DFS)

DFS is a traversal algorithm that is implemented using a stack. The following are the steps of DFS,

1. Select an unvisited node, visit the node, and treat it as the current node.
2. Select an unvisited neighbor node of the current node, visit it and make that node the new current node.
3. Repeat step 2 until there are no unvisited neighbor of the current node.
4. Backtrack to the parent node and make it the new current node. Go to step 2.

Breadth-First Search (BFS)

BFS is a traversal algorithm that is implemented using a queue. The following are the steps of BFS,

1. Select an unvisited node, visit the node, and make it as the current node.
2. Move horizontally and visit all the nodes at the next level of the current node.
3. Repeat step 2 until all there are no unvisited nodes.

Context and Applications

This topic is important for postgraduate and undergraduate courses, particularly for, Bachelor's in Computer Science Engineering, and an Associate of Science in Computer Science.

Practice Problems

Question 1: ___ is the time taken to obtain the adjacent list vertices.

1. O(1)
2. O(E)
3. O(V)
4. None of the above

Answer: Option a is correct.

Explanation: The time taken to get the adjacent list vertices is O(1) and this acts as an advantage for several algorithms.

Question 2:  ___ is used to store the Facebook data.

1. Data science
2. Graph data structure
3. Adjacency list representation
4. Subgraph representation

Answer: Option b is correct.

Explanation: Facebook is an example of a graph. The graph data structure is used to store the Facebook data and Facebook is a collection of edges and nodes.

Question 3: A graph is represented by using ______.

1. Directed and undirected graph
2. Adjacent matrix and adjacent list
3. Cyclic and acyclic graph
4. None of the above

Answer: Option b is correct.

Explanation: The adjacent matrix and adjacent list are the two data structures for graph representation. Depending on the complexity a method will be selected.

Question 4: Two standard graph traversal techniques are ___ and ___.

1. BFS and DFS
2. In order and preorder traversal
3. Postorder traversal and BFS
4. Postorder traversal and DFS

Answer: Option a is correct.

Explanation: The graph traversal technique visits each and every node exactly once in a systematic fashion. The two methods of graph traversal are BFS and DFS.

Question 5: A graph with a ____ path is known as a cyclic graph.

1. Weighted
2. Closed
3. Open
4. None of the above

Answer: Option b is correct.

Explanation: When a graph contains a closed path, then the graph is known as cyclic. A graph with no cycle is called an acyclic graph. A closed path starts from one vertex and ends on the same vertex.