CALCULUS AND ITS APPLICATIONS BRIEF
12th Edition
ISBN: 9780135998229
Author: BITTINGER
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter R.3, Problem 4E
To determine
The interval notation for the given graph.
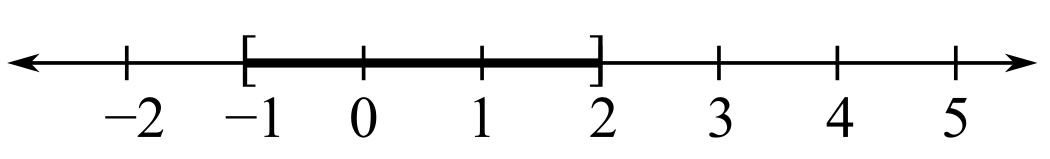
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A ladder 25 feet long is leaning against the wall of a building. Initially, the foot of the ladder is 7 feet from the wall. The foot of the ladder begins to slide at a rate of 2 ft/sec, causing the top of the ladder to slide down the wall. The location of the foot of the ladder, its x coordinate, at time t seconds is given by
x(t)=7+2t.
wall
y(1)
25 ft. ladder
x(1)
ground
(a) Find the formula for the location of the top of the ladder, the y coordinate, as a function of time t. The formula for y(t)= √ 25² - (7+2t)²
(b) The domain of t values for y(t) ranges from 0
(c) Calculate the average velocity of the top of the ladder on each of these time intervals (correct to three decimal places):
. (Put your cursor in the box, click and a palette will come up to help you enter your symbolic answer.)
time interval
ave velocity
[0,2]
-0.766
[6,8]
-3.225
time interval
ave velocity
-1.224
-9.798
[2,4]
[8,9]
(d) Find a time interval [a,9] so that the average velocity of the top of the ladder on this…
Total marks 15
3.
(i)
Let FRN Rm be a mapping and x = RN is a given
point. Which of the following statements are true? Construct counterex-
amples for any that are false.
(a)
If F is continuous at x then F is differentiable at x.
(b)
If F is differentiable at x then F is continuous at x.
If F is differentiable at x then F has all 1st order partial
(c)
derivatives at x.
(d) If all 1st order partial derivatives of F exist and are con-
tinuous on RN then F is differentiable at x.
[5 Marks]
(ii) Let mappings
F= (F1, F2) R³ → R² and
G=(G1, G2) R² → R²
:
be defined by
F₁ (x1, x2, x3) = x1 + x²,
G1(1, 2) = 31,
F2(x1, x2, x3) = x² + x3,
G2(1, 2)=sin(1+ y2).
By using the chain rule, calculate the Jacobian matrix of the mapping
GoF R3 R²,
i.e., JGoF(x1, x2, x3). What is JGOF(0, 0, 0)?
(iii)
[7 Marks]
Give reasons why the mapping Go F is differentiable at
(0, 0, 0) R³ and determine the derivative matrix D(GF)(0, 0, 0).
[3 Marks]
5.
(i)
Let f R2 R be defined by
f(x1, x2) = x² - 4x1x2 + 2x3.
Find all local minima of f on R².
(ii)
[10 Marks]
Give an example of a function f: R2 R which is not bounded
above and has exactly one critical point, which is a minimum. Justify briefly
Total marks 15
your answer.
[5 Marks]
Chapter R Solutions
CALCULUS AND ITS APPLICATIONS BRIEF
Ch. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - Prob. 2ECh. R.1 - Prob. 3ECh. R.1 - Prob. 4ECh. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - Prob. 7ECh. R.1 - Prob. 8ECh. R.1 - Prob. 9ECh. R.1 - In Exercises 1-22, graph each equation. Use a...
Ch. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - Prob. 13ECh. R.1 - Prob. 14ECh. R.1 - Prob. 15ECh. R.1 - Prob. 16ECh. R.1 - Prob. 17ECh. R.1 - Prob. 18ECh. R.1 - Prob. 19ECh. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - Medicine. Ibuprofen is a medication used to...Ch. R.1 - Running records. According to at least one study,...Ch. R.1 - Optimum solar panel angle. The optimum angle A, in...Ch. R.1 - Rise in sea level. The rise in sea level t years...Ch. R.1 - Prob. 27ECh. R.1 - Use the model N=0.0011t2+0.0412t+3.032, where t is...Ch. R.1 - Snowboarding in the half-pipe. Shaun White, The...Ch. R.1 - Prob. 30ECh. R.1 - Compound interest. Southside Investments purchases...Ch. R.1 - Prob. 32ECh. R.1 - Compound interest. Stateside Brokers deposit...Ch. R.1 - Compound interest. The Kims deposit $1000 in Wiles...Ch. R.1 - Determining monthly loan payments. If P dollars...Ch. R.1 - Determining monthly loan payments. If P dollars...Ch. R.1 - Annuities. If P dollars are invested annually in...Ch. R.1 - Annuities. If P dollars are invested annually in...Ch. R.1 - Unemployment rate. The unemployment rate in the...Ch. R.1 - Prob. 40ECh. R.1 - Annual yield. The annual interest rate r, when...Ch. R.1 - Prob. 44ECh. R.1 - Prob. 45ECh. R.1 - Annual yield. The annual interest rate r, when...Ch. R.1 - Prob. 47ECh. R.1 - Chris is considering two savings accounts: Sierra...Ch. R.1 - Prob. 49ECh. R.1 - Prob. 50ECh. R.1 - Prob. 51ECh. R.1 - The Technology Connection heading indicates...Ch. R.2 - Note: A review of algebra can be found in Appendix...Ch. R.2 - Note: A review of algebra can be found in Appendix...Ch. R.2 - Note: A review of algebra can be found in Appendix...Ch. R.2 - Note: A review of algebra can be found in Appendix...Ch. R.2 - Note: A review of algebra can be found in Appendix...Ch. R.2 - Note: A review of algebra can be found in Appendix...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - 19. A function f is given by
.
This function...Ch. R.2 - A function f is given by f(x)=3x+2 This function...Ch. R.2 - A function g is given by g(x)=x23. Find...Ch. R.2 - A function g is given by g(x)=x2+4. Find...Ch. R.2 - A function f is given by f(x)=1(x+3)2. Find...Ch. R.2 - A function f is given by f(x)=1(x5)2. This...Ch. R.2 - A function f takes a number x, multiples it by 4,...Ch. R.2 - A function g takes a number x, multiples it by 3,...Ch. R.2 - 27. A function h takes a number x. squares it, and...Ch. R.2 - 28. A function k takes a number x, squares it, and...Ch. R.2 - Graph each function. f(x)=2x5Ch. R.2 - Graph each function. f(x)=3x1Ch. R.2 - Graph each function.
31.
Ch. R.2 - Graph each function.
32.
Ch. R.2 - Graph each function.
33.
Ch. R.2 - Graph each function.
34.
Ch. R.2 - Graph each function. f(x)=6x2Ch. R.2 - Graph each function. g(x)=x2+1Ch. R.2 - Graph each function.
37.
Ch. R.2 - Graph each function.
38.
Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - In Exercises 57 and 58, assume that x is the input...Ch. R.2 - In Exercises 57 and 58, assume that x is the input...Ch. R.2 - 55. For , find .
Ch. R.2 - 56. For , and .
Ch. R.2 - For Exercises 57-60, Consider the function f given...Ch. R.2 - For Exercises 57-60, Consider the function f given...Ch. R.2 - For Exercises 57-60, Consider the function f given...Ch. R.2 - For Exercises 57-60, Consider the function f given...Ch. R.2 - Graph. f(x)={1,forx0,1,forx0Ch. R.2 - Graph.
62.
Ch. R.2 - Graph. f(x)={6,forx3,6,forx=2,Ch. R.2 - Graph. f(x)={5,forx=1,x3,forx=1,Ch. R.2 - Graph.
65.
Ch. R.2 - Graph.
66.
Ch. R.2 - Graph.
67.
Ch. R.2 - Graph.
68.
Ch. R.2 - Graph. f(x)={7,forx=2,x23,forx2Ch. R.2 - Graph. f(x)={6,forx=3,x2+5,forx3Ch. R.2 - The amount of money, A(t), in a savings account...Ch. R.2 - The amount of money, A(t), in a savings account...Ch. R.2 - Prob. 77ECh. R.2 - Prob. 78ECh. R.2 - Scaling stress factors. In psychology a process...Ch. R.2 - Solve for y in terms of x, and determine if the...Ch. R.2 - Solve for y in terms of x, and determine if the...Ch. R.2 - Solve for y in terms of x, and determine if the...Ch. R.2 - Solve for y in terms of x, and determine if the...Ch. R.2 - Explain why the vertical-line test works.Ch. R.2 - Prob. 86ECh. R.2 - In Exercises 82 and 83, use the table feature to...Ch. R.2 - In Exercises 82 and 83, use the table feature to...Ch. R.2 - 86. A function f takes a number x, adds 2, and...Ch. R.2 - 87. A function f takes a number x, adds 2, and...Ch. R.2 -
89. A function f takes a number x, multiplies it...Ch. R.2 - Prob. 94ECh. R.3 - Prob. 1ECh. R.3 - Prob. 2ECh. R.3 - Prob. 3ECh. R.3 - Prob. 4ECh. R.3 - Prob. 5ECh. R.3 - Prob. 6ECh. R.3 - Prob. 7ECh. R.3 - Prob. 8ECh. R.3 - Prob. 9ECh. R.3 - In Exercises 1-10, write interval notation for...Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Prob. 20ECh. R.3 - In Exercises 21 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 32, each graph is that of a...Ch. R.3 - Write the domain of each function given below in...Ch. R.3 - Write the domain of each function given below in...Ch. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 36ECh. R.3 - Prob. 37ECh. R.3 - Prob. 38ECh. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 40ECh. R.3 - Prob. 41ECh. R.3 - Prob. 42ECh. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 44ECh. R.3 - Write the domain of each function given below in...Ch. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 47ECh. R.3 - Prob. 48ECh. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 50ECh. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 52ECh. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 54ECh. R.3 - Prob. 55ECh. R.3 - Prob. 56ECh. R.3 - Prob. 57ECh. R.3 - Prob. 58ECh. R.3 - Prob. 59ECh. R.3 - Prob. 60ECh. R.3 - Hourly earnings. Karen works as a contractor,...Ch. R.3 - Sales tax. Marcus plans to spend at most $200 at...Ch. R.3 - Prob. 63ECh. R.3 - Prob. 64ECh. R.3 - Prob. 65ECh. R.3 - Prob. 67ECh. R.3 - Prob. 68ECh. R.3 - Prob. 69ECh. R.3 - Prob. 70ECh. R.3 - Prob. 71ECh. R.3 - Write an equation for a function whose domain is...Ch. R.3 - Prob. 73ECh. R.3 - Prob. 74ECh. R.3 - Prob. 75ECh. R.3 - Prob. 76ECh. R.4 - Graph. List the slope and y-intercept. 1. y=2xCh. R.4 - Prob. 2ECh. R.4 - Prob. 3ECh. R.4 - Prob. 4ECh. R.4 - Prob. 5ECh. R.4 - Graph. List the slope and y-intercept. 6. y=2x5Ch. R.4 - Graph. List the slope and y-intercept. 7....Ch. R.4 - Prob. 8ECh. R.4 - Prob. 9ECh. R.4 - Prob. 10ECh. R.4 - Find the slope and y-intercept. y4x=1Ch. R.4 - Find the slope and y-intercept. y3x=6Ch. R.4 - Find the slope and y-intercept. 2x+y3=0Ch. R.4 - Find the slope and y-intercept.
22.
Ch. R.4 - Find the slope and y-intercept. 3x3y+6=0Ch. R.4 - Find the slope and y-intercept.
24.
Ch. R.4 - Find the slope and y-intercept. x=3y+7Ch. R.4 - Find the slope and y-intercept. x=4y+3Ch. R.4 - For Exercises 19-28, use the given point and slope...Ch. R.4 - Prob. 20ECh. R.4 - For Exercises 19-28, use the given point and slope...Ch. R.4 - Prob. 22ECh. R.4 - For Exercises 19-28, use the given point and slope...Ch. R.4 - For Exercises 19-28, use the given point and slope...Ch. R.4 - For Exercises 19-28, use the given point and slope...Ch. R.4 - Prob. 26ECh. R.4 - Prob. 27ECh. R.4 - Prob. 28ECh. R.4 - For Exercises 29-50, find (a) the slope (if it is...Ch. R.4 - Prob. 30ECh. R.4 - Prob. 31ECh. R.4 - Prob. 32ECh. R.4 - For Exercises 29-50, find (a) the slope (if it is...Ch. R.4 - Prob. 34ECh. R.4 - Prob. 35ECh. R.4 - Prob. 36ECh. R.4 - Prob. 37ECh. R.4 - Prob. 38ECh. R.4 - Prob. 39ECh. R.4 - Prob. 40ECh. R.4 - For Exercises 29-50, find (a) the slope (if it is...Ch. R.4 - For Exercises 29-50, find (a) the slope (if it is...Ch. R.4 - For Exercises 29-50, find (a) the slope (if it is...Ch. R.4 - Prob. 44ECh. R.4 - Prob. 45ECh. R.4 - Prob. 46ECh. R.4 - For Exercises 29-50, find (a) the slope (if it is...Ch. R.4 - Prob. 48ECh. R.4 - Prob. 49ECh. R.4 - Prob. 50ECh. R.4 - 61. Find the slope (or grade) of the treadmill.
Ch. R.4 - Find the slope of the skateboard ramp.Ch. R.4 - Find the slope (or head) of the river. Express the...Ch. R.4 - Prob. 54ECh. R.4 - Prob. 55ECh. R.4 - Prob. 56ECh. R.4 - Highway tolls. It has been suggested that since...Ch. R.4 - Inkjet cartridges. A registrar's office finds that...Ch. R.4 - Prob. 59ECh. R.4 - Profit-and-loss analysis. Red Tide is planning a...Ch. R.4 - Profit-and-loss analysis. Raven Entertainment...Ch. R.4 - Straight-line depreciation. Quick Copy buys an...Ch. R.4 - Prob. 64ECh. R.4 - Prob. 65ECh. R.4 - 72. Straight-line depreciation. Tyline Electric...Ch. R.4 - Stair requirements. A North Carolina state law...Ch. R.4 - Prob. 68ECh. R.4 - Health insurance premiums. Find the average rate...Ch. R.4 - Prob. 70ECh. R.4 - Prob. 71ECh. R.4 - Prob. 72ECh. R.4 - Energy conservation. The R-factor of home...Ch. R.4 - Nerve impulse speed. Impulses in nerve fibers...Ch. R.4 - Muscle weight. The weight M of a persons muscles...Ch. R.4 - 81. Brain weight. The weight B of a person's brain...Ch. R.4 - Prob. 77ECh. R.4 - 83. Reaction time. While driving a car, you see a...Ch. R.4 - Estimating heights. An anthropologist can use...Ch. R.4 - Prob. 80ECh. R.4 - Prob. 82ECh. R.4 - Prob. 83ECh. R.4 - 89. Suppose, and all lie on the same line. Find...Ch. R.4 - Describe one situation in which you would use the...Ch. R.4 - Business: daily sales. Match each sentence below...Ch. R.4 - Business: depreciation. A large crane is being...Ch. R.4 - Graph some of the total-revenue, total-cost, and...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Prob. 2ECh. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Prob. 9ECh. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Prob. 14ECh. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Prob. 16ECh. R.5 - For each of the following quadratic functions, (a)...Ch. R.5 - Prob. 18ECh. R.5 - Prob. 19ECh. R.5 - For each of the following quadratic functions, (a)...Ch. R.5 - For each of the following quadratic functions, (a)...Ch. R.5 - For each of the following quadratic functions, (a)...Ch. R.5 - For each of the following quadratic functions, (a)...Ch. R.5 - Prob. 24ECh. R.5 - Prob. 25ECh. R.5 - Prob. 26ECh. R.5 - Graph, and state the domain using interval...Ch. R.5 - Prob. 28ECh. R.5 - Graph, and state the domain using interval...Ch. R.5 - Graph, and state the domain using interval...Ch. R.5 - Graph, and state the domain using interval...Ch. R.5 - Graph, and state the domain using interval...Ch. R.5 - Graph, and state the domain using interval...Ch. R.5 - Prob. 34ECh. R.5 - Solve. x22x=2Ch. R.5 - Solve. x22x+1=5Ch. R.5 - Solve.
47.
Ch. R.5 - Solve. x2+4x=3Ch. R.5 - Solve. 4x2=4x+1Ch. R.5 - Solve.
50.
Ch. R.5 - Solve. 3y2+8y+2=0Ch. R.5 - Solve. 2p25p=1Ch. R.5 - Solve. x+7+9x=0 (Hint: Multiply both sides by x).Ch. R.5 - Solve. 11w=1w2Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Prob. 46ECh. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Prob. 56ECh. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Prob. 62ECh. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Simplify.
75.
Ch. R.5 - Simplify.
76.
Ch. R.5 - Simplify.
77.
Ch. R.5 - Simplify. 82/3Ch. R.5 - Determine the domain of each function. f(x)=x225x5Ch. R.5 - Determine the domain of each function. f(x)=x24x+2Ch. R.5 - Determine the domain of each function....Ch. R.5 - Determine the domain of each function....Ch. R.5 - Determine the domain of each function. f(x)=5x+4Ch. R.5 - Determine the domain of each function. f(x)=2x6Ch. R.5 - Determine the domain of each function.
85.
Ch. R.5 - Determine the domain of each function.
86.
Ch. R.5 - Prob. 77ECh. R.5 - Prob. 78ECh. R.5 - Prob. 79ECh. R.5 - Find the equilibrium point for each pair of demand...Ch. R.5 - Find the equilibrium point for each pair of demand...Ch. R.5 - Prob. 82ECh. R.5 - Prob. 83ECh. R.5 - Find the equilibrium point for each pair of demand...Ch. R.5 - 95. Price of admission. The number of tickets sold...Ch. R.5 - Demand. The quantity sold x of a high-definition...Ch. R.5 - 97. Radar Range. The function given by
can be...Ch. R.5 - Find the equilibrium point for each pair of demand...Ch. R.5 - 99. Life Science: pollution control. Pollution...Ch. R.5 - Surface area and mass. The surface area of a...Ch. R.5 - Prob. 91ECh. R.5 - At most, how many y-intercepts can a function...Ch. R.5 - What is the difference between a rational function...Ch. R.5 - Prob. 94ECh. R.5 - Prob. 95ECh. R.5 - Prob. 96ECh. R.5 - Prob. 97ECh. R.5 - Prob. 98ECh. R.5 - Prob. 99ECh. R.5 - Prob. 100ECh. R.5 - Prob. 101ECh. R.5 - Prob. 102ECh. R.5 - Prob. 103ECh. R.5 - Prob. 104ECh. R.5 - Prob. 105ECh. R.5 - Prob. 106ECh. R.6 - For Exercises 1-10, (a) complete an input-output...Ch. R.6 - Prob. 2ECh. R.6 - Prob. 3ECh. R.6 - For Exercises 1-10, (a) complete an input-output...Ch. R.6 - Prob. 5ECh. R.6 - For Exercises 1-10, (a) complete an input-output...Ch. R.6 - Prob. 7ECh. R.6 - Prob. 8ECh. R.6 - Prob. 9ECh. R.6 - Prob. 10ECh. R.6 - Write an equivalent logarithmic equation. 11....Ch. R.6 - Write an equivalent logarithmic equation. 12....Ch. R.6 - Prob. 13ECh. R.6 - Write an equivalent logarithmic equation. 14....Ch. R.6 - Prob. 15ECh. R.6 - Write an equivalent logarithmic equation. 16. 36=6Ch. R.6 - Prob. 17ECh. R.6 - Write an equivalent logarithmic equation. 18....Ch. R.6 - Prob. 19ECh. R.6 - Write an equivalent logarithmic equation. 20. rv=zCh. R.6 - Prob. 21ECh. R.6 - Prob. 22ECh. R.6 - Prob. 23ECh. R.6 - Prob. 24ECh. R.6 - Write an equivalent exponential equation. 25....Ch. R.6 - Write an equivalent exponential equation. 26....Ch. R.6 - Prob. 27ECh. R.6 - Write an equivalent exponential equation. 28....Ch. R.6 - Prob. 29ECh. R.6 - Prob. 30ECh. R.6 - Solve for x without using a calculator. 31....Ch. R.6 - Solve for x without using a calculator. 32....Ch. R.6 - Prob. 33ECh. R.6 - Solve for x without using a calculator. 34....Ch. R.6 - Solve for x without using a calculator. 35....Ch. R.6 - Prob. 36ECh. R.6 - Solve for x without using a calculator. 37....Ch. R.6 - Prob. 38ECh. R.6 - Prob. 39ECh. R.6 - Solve for x without using a calculator. 40....Ch. R.6 - Use the change-of-base formula to find each...Ch. R.6 - Use the change-of-base formula to find each...Ch. R.6 - Prob. 43ECh. R.6 - Prob. 44ECh. R.6 - Prob. 45ECh. R.6 - Use the change-of-base formula to find each...Ch. R.6 - Prob. 47ECh. R.6 - Prob. 48ECh. R.6 - Use the change-of-base formula to find each...Ch. R.6 - Use the change-of-base formula to find each...Ch. R.6 - Prob. 51ECh. R.6 - Solve each equation for x. Give the answers to...Ch. R.6 - Prob. 53ECh. R.6 - Prob. 54ECh. R.6 - Prob. 55ECh. R.6 - Prob. 56ECh. R.6 - Prob. 57ECh. R.6 - Prob. 58ECh. R.6 - Solve each equation for x. Give the answers to...Ch. R.6 - Solve each equation for x. Give the answers to...Ch. R.6 - Given loga2=0.483 and loga3=0.766, use the...Ch. R.6 - Prob. 62ECh. R.6 - Prob. 63ECh. R.6 - Given loga2=0.483 and loga3=0.766, use the...Ch. R.6 - Given loga2=0.483 and loga3=0.766, use the...Ch. R.6 - Given loga2=0.483 and loga3=0.766, use the...Ch. R.6 - Prob. 67ECh. R.6 - Given loga2=0.483 and loga3=0.766, use the...Ch. R.6 - Prob. 69ECh. R.6 - Given loga2=0.483 and loga3=0.766, use the...Ch. R.6 - Sketch the graph of each logarithmic function, and...Ch. R.6 - Sketch the graph of each logarithmic function, and...Ch. R.6 - Prob. 73ECh. R.6 - Prob. 74ECh. R.6 - Prob. 75ECh. R.6 - Sketch the graph of each logarithmic function, and...Ch. R.6 - Casa Grande Technical School had a total...Ch. R.6 - Parker Valley had a population of 12,500 in 2015,...Ch. R.6 - An element undergoes natural radioactive decay....Ch. R.6 - Prob. 80ECh. R.6 - The online program at Accent University had an...Ch. R.6 - The startup GorePoint Inc. had 15 employees...Ch. R.6 - Prob. 83ECh. R.6 - Jenny deposits $5000 into a savings account that...Ch. R.6 - A stock originally worth $50 per share is losing 1...Ch. R.6 - A property originally worth $12,000 is losing 3 of...Ch. R.6 - Prob. 87ECh. R.6 - Prob. 88ECh. R.6 - Prob. 89ECh. R.6 - Prob. 90ECh. R.6 - Prob. 91ECh. R.6 - Prob. 92ECh. R.6 - Prob. 93ECh. R.7 - For the scatter plots and graphs in Exercises 1 9,...Ch. R.7 - For the scatter plots and graphs in Exercises 1 9,...Ch. R.7 - For the scatter plots and graphs in Exercises 1 9,...Ch. R.7 - Prob. 4ECh. R.7 - Prob. 5ECh. R.7 - Prob. 6ECh. R.7 - Prob. 7ECh. R.7 - Prob. 8ECh. R.7 - Prob. 9ECh. R.7 - Average salary in NBA. Use the data from the bar...Ch. R.7 - Prob. 11ECh. R.7 - Absorption of an asthma medication. Use the data...Ch. R.7 - Median household income. Use the data given in...Ch. R.7 - Braking Distance. y=0.144x24.63x+60 Find a...Ch. R.7 - High blood pressure in women. a) Use the first and...Ch. R.7 - Prob. 16ECh. R.7 - Prob. 17ECh. R.7 - Prob. 18ECh. R.7 - Prob. 19ECh. R.7 - In Exercises 17-20, round the numbers in each...Ch. R.7 - 21. Under what conditions might it make better...Ch. R.7 - Prob. 23ECh. R.7 - Prob. 27ECh. R - These review exercises are for test preparation....Ch. R - These review exercises are for test preparation....Ch. R - These review exercises are for test preparation....Ch. R - Prob. 4RECh. R - Prob. 5RECh. R - Prob. 6RECh. R - Prob. 7RECh. R - Prob. 8RECh. R - In Exercises 8 14, classify each statement as...Ch. R - In Exercises 8 14, classify each statement as...Ch. R - Prob. 11RECh. R - In Exercises 8 14, classify each statement as...Ch. R - In Exercises 8 14, classify each statement as...Ch. R - Prob. 14RECh. R - In Exercises 8 – 14, classify each statement as...Ch. R - 15. Hearing-impaired Americans. The following...Ch. R - Finance: compound interest. Sam borrows $4000 at...Ch. R - Business: compound interest. Lucinda invests...Ch. R - Is the following correspondence a function? Why or...Ch. R - A function is given by f(x)=x2+x. Find each of the...Ch. R - Graph. [R.5] f(x)=(x2)2Ch. R - Graph. [R.5] 22. y=x1Ch. R - Graph. [R.5] 23. f(x)=3xx+4Ch. R - Graph. [R.5] g(x)=x+1Ch. R - Use the vertical-line test to determine whether...Ch. R - Use the vertical-line test to determine whether...Ch. R - Use the vertical-line test to determine whether...Ch. R - Use the vertical-line test to determine whether...Ch. R - For the graph of function f shown to the right...Ch. R - 29. Consider the function given by
a. Find ...Ch. R - Use the vertical-line test to determine whether...Ch. R - Write interval notation for each of the following....Ch. R - For the function graphed below, determine (a)...Ch. R - Use the vertical-line test to determine whether...Ch. R - 34. What are the slope and the y-intercept of?
Ch. R - 35. Find an equation of the line with slope,...Ch. R - Find the slope of the line containing the points...Ch. R - Find the average rate of change.
37.
Ch. R - Find the average rate of change. [R.4]Ch. R - Business: shipping charges. The amount A that...Ch. R - 40. Business: profit-and-loss analysis. The band...Ch. R - Prob. 42RECh. R - Graph each of the following. If the graph is a...Ch. R - Solve each of the following. [R.5] a. 5+x2=4x+2 b....Ch. R - Prob. 45RECh. R - 45. Rewrite each of the following as an equivalent...Ch. R - Determine the domain of the function given by...Ch. R - Prob. 48RECh. R - The population of Arvon Hill is given by...Ch. R - Prob. 50RECh. R - Given logb2=0.314 and logb3=0.497: [R.6] a) Find...Ch. R - Prob. 52RECh. R - Prob. 53RECh. R - Prob. 54RECh. R - Prob. 55RECh. R - Prob. 56RECh. R - 52. Economics: demand. The demand function for...Ch. R - Prob. 58RECh. R - Prob. 59RECh. R - Prob. 60RECh. R - Prob. 61RECh. R - Prob. 62RECh. R - Prob. 63RECh. R - Prob. 64RECh. R - Business: compound interest. Cecilia invests funds...Ch. R - Prob. 2TCh. R - Find the slope and they-intercept of the graph of...Ch. R - 4. Find an equation of the line with slope,...Ch. R - Find the slope of the line containing the points...Ch. R - Find the average rate of change.Ch. R - Find the average rate of change.
7.
Ch. R - Life Science: body fluids. The weight F of fluids...Ch. R - 9. Business: profit-and-loss analysis. A printing...Ch. R - Prob. 10TCh. R - Use the vertical-line test to determine whether...Ch. R - Use the vertical-line test to determine whether...Ch. R - 13. For the following graph of a quadratic...Ch. R - Graph: f(x)=8/x.Ch. R - Prob. 15TCh. R - Prob. 16TCh. R - Prob. 17TCh. R - Prob. 18TCh. R - 20. Write interval notation for the following...Ch. R - Prob. 20TCh. R - Prob. 21TCh. R - Graph: f(x)={x2+2,forx0,x22,forx0.Ch. R - Graph and identify the y-intercept: f(x)=12(3)x.Ch. R - Prob. 24TCh. R - Nutrition. As people age their daily caloric needs...Ch. R - 24. Simplify: .
Ch. R - 25. Find the domain and the zeros of the function...Ch. R - Prob. 28TCh. R - 27. A function's average rate of change over the...Ch. R - Graph f and find its zeros, domain, and range:...Ch. R - Prob. 31T
Additional Math Textbook Solutions
Find more solutions based on key concepts
Whether the requirements for a hypothesis test are satisfied or not.
Elementary Statistics
Regression and Predictions. Exercises 13–28 use the same data sets as Exercises 13–28 in Section 10-1. In each ...
Elementary Statistics (13th Edition)
Fill in each blank so that the resulting statement is true. An equation that expresses a relationship between t...
Algebra and Trigonometry (6th Edition)
Voting A random sample of likely voters showed that 49 planned to support Measure X. The margin of error is 3 p...
Introductory Statistics
The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...
Basic Business Statistics, Student Value Edition
Find the additive inverse of each of the following integers. Write the answer in the simplest possible form. a....
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Total marks 15 4. : Let f R2 R be defined by f(x1, x2) = 2x²- 8x1x2+4x+2. Find all local minima of f on R². [10 Marks] (ii) Give an example of a function f R2 R which is neither bounded below nor bounded above, and has no critical point. Justify briefly your answer. [5 Marks]arrow_forward4. Let F RNR be a mapping. (i) x ЄRN ? (ii) : What does it mean to say that F is differentiable at a point [1 Mark] In Theorem 5.4 in the Lecture Notes we proved that if F is differentiable at a point x E RN then F is continuous at x. Proof. Let (n) CRN be a sequence such that xn → x ЄERN as n → ∞. We want to show that F(xn) F(x), which means F is continuous at x. Denote hnxn - x, so that ||hn|| 0. Thus we find ||F(xn) − F(x)|| = ||F(x + hn) − F(x)|| * ||DF (x)hn + R(hn) || (**) ||DF(x)hn||+||R(hn)||| → 0, because the linear mapping DF(x) is continuous and for all large nЄ N, (***) ||R(hn) || ||R(hn) || ≤ → 0. ||hn|| (a) Explain in details why ||hn|| → 0. [3 Marks] (b) Explain the steps labelled (*), (**), (***). [6 Marks]arrow_forward4. In Theorem 5.4 in the Lecture Notes we proved that if F: RN → Rm is differentiable at x = RN then F is continuous at x. Proof. Let (xn) CRN be a sequence such that x → x Є RN as n → ∞. We want F(x), which means F is continuous at x. to show that F(xn) Denote hn xnx, so that ||hn||| 0. Thus we find ||F (xn) − F(x) || (*) ||F(x + hn) − F(x)|| = ||DF(x)hn + R(hn)|| (**) ||DF(x)hn|| + ||R(hn) || → 0, because the linear mapping DF(x) is continuous and for all large n = N, |||R(hn) || ≤ (***) ||R(hn)|| ||hn|| → 0. Explain the steps labelled (*), (**), (***) [6 Marks] (ii) Give an example of a function F: RR such that F is contin- Total marks 10 uous at x=0 but F is not differentiable at at x = 0. [4 Marks]arrow_forward
- 3. Let f R2 R be a function. (i) Explain in your own words the relationship between the existence of all partial derivatives of f and differentiability of f at a point x = R². (ii) Consider R2 → R defined by : [5 Marks] f(x1, x2) = |2x1x2|1/2 Show that af af -(0,0) = 0 and -(0, 0) = 0, Jx1 მx2 but f is not differentiable at (0,0). [10 Marks]arrow_forward(1) Write the following quadratic equation in terms of the vertex coordinates.arrow_forwardThe final answer is 8/π(sinx) + 8/3π(sin 3x)+ 8/5π(sin5x)....arrow_forward
- Keity x२ 1. (i) Identify which of the following subsets of R2 are open and which are not. (a) A = (2,4) x (1, 2), (b) B = (2,4) x {1,2}, (c) C = (2,4) x R. Provide a sketch and a brief explanation to each of your answers. [6 Marks] (ii) Give an example of a bounded set in R2 which is not open. [2 Marks] (iii) Give an example of an open set in R2 which is not bounded. [2 Marksarrow_forward2. (i) Which of the following statements are true? Construct coun- terexamples for those that are false. (a) sequence. Every bounded sequence (x(n)) nEN C RN has a convergent sub- (b) (c) (d) Every sequence (x(n)) nEN C RN has a convergent subsequence. Every convergent sequence (x(n)) nEN C RN is bounded. Every bounded sequence (x(n)) EN CRN converges. nЄN (e) If a sequence (xn)nEN C RN has a convergent subsequence, then (xn)nEN is convergent. [10 Marks] (ii) Give an example of a sequence (x(n))nEN CR2 which is located on the parabola x2 = x², contains infinitely many different points and converges to the limit x = (2,4). [5 Marks]arrow_forward2. (i) What does it mean to say that a sequence (x(n)) nEN CR2 converges to the limit x E R²? [1 Mark] (ii) Prove that if a set ECR2 is closed then every convergent sequence (x(n))nen in E has its limit in E, that is (x(n)) CE and x() x x = E. [5 Marks] (iii) which is located on the parabola x2 = = x x4, contains a subsequence that Give an example of an unbounded sequence (r(n)) nEN CR2 (2, 16) and such that x(i) converges to the limit x = (2, 16) and such that x(i) # x() for any i j. [4 Marksarrow_forward
- 1. (i) which are not. Identify which of the following subsets of R2 are open and (a) A = (1, 3) x (1,2) (b) B = (1,3) x {1,2} (c) C = AUB (ii) Provide a sketch and a brief explanation to each of your answers. [6 Marks] Give an example of a bounded set in R2 which is not open. (iii) [2 Marks] Give an example of an open set in R2 which is not bounded. [2 Marks]arrow_forward2. if limit. Recall that a sequence (x(n)) CR2 converges to the limit x = R² lim ||x(n)x|| = 0. 818 - (i) Prove that a convergent sequence (x(n)) has at most one [4 Marks] (ii) Give an example of a bounded sequence (x(n)) CR2 that has no limit and has accumulation points (1, 0) and (0, 1) [3 Marks] (iii) Give an example of a sequence (x(n))neN CR2 which is located on the hyperbola x2 1/x1, contains infinitely many different Total marks 10 points and converges to the limit x = (2, 1/2). [3 Marks]arrow_forward3. (i) Consider a mapping F: RN Rm. Explain in your own words the relationship between the existence of all partial derivatives of F and dif- ferentiability of F at a point x = RN. (ii) [3 Marks] Calculate the gradient of the following function f: R2 → R, f(x) = ||x||3, Total marks 10 where ||x|| = √√√x² + x/2. [7 Marks]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL