PRECALCULUS:GRAPH...-NASTA ED.(FLORIDA)
PRECALCULUS:GRAPH...-NASTA ED.(FLORIDA)
10th Edition
ISBN: 9780136174318
Author: Demana
Publisher: PEARSON
bartleby

Videos

Expert Solution & Answer
Book Icon
Chapter P.2, Problem 55E
Solution

Prove that the midpoint of the hypotenuse of the right triangle with vertices (0, 0), (5, 0), and (0, 7) is equidistant from the three vertices.

AD=CD=BD= 18.5

The Mid-point of right triangle is equidistant from all the three vertices.

Given information:

Vertices of right triangle are (0, 0), (5, 0), and (0, 7)

Concept used:

  • First, find the value for x on the x-axis.
  • Next, find the y-value on the y-axis.
  • The point should be plotted at the intersection of x and y.
  • Finally, plot the point on your graph at the appropriate spot.
  • Then join all the points to make a closed figure.

Calculation:

The given points are A(0, 0), B(5, 0), and C(0, 7)

Plotting the points in the graph -

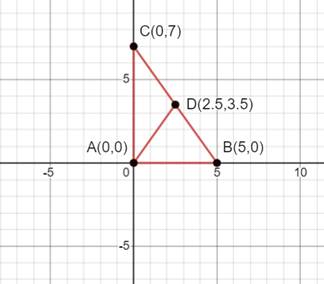
  PRECALCULUS:GRAPH...-NASTA ED.(FLORIDA), Chapter P.2, Problem 55E

The mid-point is D(2.5, 3.5).

Using distance formula −

A(0, 0), D(2.5, 3.5)

  AD=(x1−x2)+(y1−y2)=(0−2.5)2+(0−3.5)2=6.25+12.25=18.5

C(0,7), D(2.5, 3.5)

  CD=(x1−x2)+(y1−y2)=(0−2.5)2+(7−3.5)2=(−2.5)2+(3.5)2=6.25+12.25=18.5

B(5, 0), D(2.5, 3.5)

  BD=(x1−x2)+(y1−y2)=(5−2.5)2+(0−3.5)2=6.25+12.25=18.5

AD=CD=BD= 18.5

As D is the mid-point of hypotenuse CB and the distance from three vertices to mid-point is same.

So mid-point of right triangle is equidistant from all the three vertices.

Previous
Chapter P.2, Problem 54E
Next
Chapter P.2, Problem 56E

Chapter P Solutions

PRECALCULUS:GRAPH...-NASTA ED.(FLORIDA)

Ch. P.1 - Prob. 1QRCh. P.1 - Prob. 2QRCh. P.1 - Prob. 3QRCh. P.1 - Prob. 4QRCh. P.1 - Prob. 5QRCh. P.1 - Prob. 6QRCh. P.1 - Prob. 7QRCh. P.1 - Prob. 8QRCh. P.1 - Prob. 9QRCh. P.1 - Prob. 10QR
Ch. P.1 - Prob. 1ECh. P.1 - Prob. 2ECh. P.1 - Prob. 3ECh. P.1 - Prob. 4ECh. P.1 - Prob. 5ECh. P.1 - Prob. 6ECh. P.1 - Prob. 7ECh. P.1 - Prob. 8ECh. P.1 - Prob. 9ECh. P.1 - Prob. 10ECh. P.1 - Prob. 11ECh. P.1 - Prob. 12ECh. P.1 - Prob. 13ECh. P.1 - Prob. 14ECh. P.1 - Prob. 15ECh. P.1 - Prob. 16ECh. P.1 - Prob. 17ECh. P.1 - Prob. 18ECh. P.1 - Prob. 19ECh. P.1 - Prob. 20ECh. P.1 - Prob. 21ECh. P.1 - Prob. 22ECh. P.1 - Prob. 23ECh. P.1 - Prob. 24ECh. P.1 - Prob. 25ECh. P.1 - Prob. 26ECh. P.1 - Prob. 27ECh. P.1 - Prob. 28ECh. P.1 - Prob. 29ECh. P.1 - Prob. 30ECh. P.1 - Prob. 31ECh. P.1 - Prob. 32ECh. P.1 - Prob. 33ECh. P.1 - Prob. 34ECh. P.1 - Prob. 35ECh. P.1 - Prob. 36ECh. P.1 - Prob. 37ECh. P.1 - Prob. 38ECh. P.1 - Prob. 39ECh. P.1 - Prob. 40ECh. P.1 - Prob. 41ECh. P.1 - Prob. 42ECh. P.1 - Prob. 43ECh. P.1 - Prob. 44ECh. P.1 - Prob. 45ECh. P.1 - Prob. 46ECh. P.1 - Prob. 47ECh. P.1 - In Exercises 4752, simplify the expression. Assume...Ch. P.1 - In Exercises 4752, simplify the expression. Assume...Ch. P.1 - Prob. 50ECh. P.1 - Prob. 51ECh. P.1 - Prob. 52ECh. P.1 - Prob. 53ECh. P.1 - Prob. 54ECh. P.1 - Prob. 55ECh. P.1 - Prob. 56ECh. P.1 - Prob. 57ECh. P.1 - Prob. 58ECh. P.1 - Prob. 59ECh. P.1 - Prob. 60ECh. P.1 - Prob. 61ECh. P.1 - Prob. 62ECh. P.1 - Prob. 63ECh. P.1 - In Exercises 63 and 64, use scientific notation to...Ch. P.1 - Prob. 65ECh. P.1 - Prob. 66ECh. P.1 - Prob. 67ECh. P.1 - Prob. 68ECh. P.1 - Prob. 69ECh. P.1 - Prob. 70ECh. P.1 - Prob. 71ECh. P.1 - Prob. 72ECh. P.1 - Prob. 73ECh. P.1 - Prob. 74ECh. P.1 - Prob. 75ECh. P.1 - Prob. 76ECh. P.2 - Prob. 1QRCh. P.2 - Prob. 2QRCh. P.2 - Prob. 3QRCh. P.2 - Prob. 4QRCh. P.2 - Prob. 5QRCh. P.2 - Prob. 6QRCh. P.2 - Prob. 7QRCh. P.2 - Prob. 8QRCh. P.2 - Prob. 9QRCh. P.2 - Prob. 10QRCh. P.2 - Prob. 1ECh. P.2 - Prob. 2ECh. P.2 - Prob. 3ECh. P.2 - Prob. 4ECh. P.2 - Prob. 5ECh. P.2 - Prob. 6ECh. P.2 - Prob. 7ECh. P.2 - Prob. 8ECh. P.2 - Prob. 9ECh. P.2 - Prob. 10ECh. P.2 - Prob. 11ECh. P.2 - Prob. 12ECh. P.2 - Prob. 13ECh. P.2 - Prob. 14ECh. P.2 - Prob. 15ECh. P.2 - Prob. 16ECh. P.2 - Prob. 17ECh. P.2 - Prob. 18ECh. P.2 - Prob. 19ECh. P.2 - Prob. 20ECh. P.2 - Prob. 21ECh. P.2 - Prob. 22ECh. P.2 - Prob. 23ECh. P.2 - Prob. 24ECh. P.2 - Prob. 25ECh. P.2 - Prob. 26ECh. P.2 - Prob. 27ECh. P.2 - Prob. 28ECh. P.2 - Prob. 29ECh. P.2 - Prob. 30ECh. P.2 - Prob. 31ECh. P.2 - Prob. 32ECh. P.2 - Prob. 33ECh. P.2 - Prob. 34ECh. P.2 - Prob. 35ECh. P.2 - Prob. 36ECh. P.2 - Prob. 37ECh. P.2 - Prob. 38ECh. P.2 - Prob. 39ECh. P.2 - Prob. 40ECh. P.2 - Prob. 41ECh. P.2 - Prob. 42ECh. P.2 - Prob. 43ECh. P.2 - Prob. 44ECh. P.2 - Prob. 45ECh. P.2 - Prob. 46ECh. P.2 - Prob. 47ECh. P.2 - Prob. 48ECh. P.2 - Prob. 49ECh. P.2 - Prob. 50ECh. P.2 - Prob. 51ECh. P.2 - Prob. 52ECh. P.2 - Prob. 53ECh. P.2 - Prob. 54ECh. P.2 - Prob. 55ECh. P.2 - Prob. 56ECh. P.2 - Prob. 57ECh. P.2 - Prob. 58ECh. P.2 - Prob. 59ECh. P.2 - Prob. 60ECh. P.2 - Prob. 61ECh. P.2 - Prob. 62ECh. P.2 - Prob. 63ECh. P.2 - Prob. 64ECh. P.2 - Prob. 65ECh. P.2 - Prob. 66ECh. P.2 - Prob. 67ECh. P.2 - Prob. 68ECh. P.2 - Prob. 69ECh. P.2 - Prob. 70ECh. P.3 - Prob. 1QRCh. P.3 - Prob. 2QRCh. P.3 - Prob. 3QRCh. P.3 - Prob. 4QRCh. P.3 - Prob. 5QRCh. P.3 - Prob. 6QRCh. P.3 - Prob. 7QRCh. P.3 - Prob. 8QRCh. P.3 - Prob. 9QRCh. P.3 - Prob. 10QRCh. P.3 - Prob. 1ECh. P.3 - Prob. 2ECh. P.3 - Prob. 3ECh. P.3 - Prob. 4ECh. P.3 - Prob. 5ECh. P.3 - Prob. 6ECh. P.3 - Prob. 7ECh. P.3 - Prob. 8ECh. P.3 - Prob. 9ECh. P.3 - Prob. 10ECh. P.3 - Prob. 11ECh. P.3 - Prob. 12ECh. P.3 - Prob. 13ECh. P.3 - Prob. 14ECh. P.3 - Prob. 15ECh. P.3 - Prob. 16ECh. P.3 - Prob. 17ECh. P.3 - Prob. 18ECh. P.3 - Prob. 19ECh. P.3 - Prob. 20ECh. P.3 - Prob. 21ECh. P.3 - Prob. 22ECh. P.3 - Prob. 23ECh. P.3 - Prob. 24ECh. P.3 - Prob. 25ECh. P.3 - Prob. 26ECh. P.3 - Prob. 27ECh. P.3 - Prob. 28ECh. P.3 - Prob. 29ECh. P.3 - Prob. 30ECh. P.3 - Prob. 31ECh. P.3 - Prob. 32ECh. P.3 - Prob. 33ECh. P.3 - Prob. 34ECh. P.3 - Prob. 35ECh. P.3 - Prob. 36ECh. P.3 - Prob. 37ECh. P.3 - Prob. 38ECh. P.3 - Prob. 39ECh. P.3 - Prob. 40ECh. P.3 - Prob. 41ECh. P.3 - Prob. 42ECh. P.3 - Prob. 43ECh. P.3 - Prob. 44ECh. P.3 - Prob. 45ECh. P.3 - Prob. 46ECh. P.3 - Prob. 47ECh. P.3 - Prob. 48ECh. P.3 - Prob. 49ECh. P.3 - Prob. 50ECh. P.3 - Prob. 51ECh. P.3 - Prob. 52ECh. P.3 - Prob. 53ECh. P.3 - Prob. 54ECh. P.3 - Prob. 55ECh. P.3 - Prob. 56ECh. P.3 - Prob. 57ECh. P.3 - Prob. 58ECh. P.3 - Prob. 59ECh. P.3 - Prob. 60ECh. P.3 - Prob. 61ECh. P.3 - Prob. 62ECh. P.3 - Prob. 63ECh. P.3 - Prob. 64ECh. P.3 - Prob. 65ECh. P.3 - Prob. 66ECh. P.3 - Prob. 67ECh. P.3 - Prob. 68ECh. P.3 - Prob. 69ECh. P.3 - Prob. 70ECh. P.3 - Prob. 71ECh. P.3 - Prob. 72ECh. P.3 - Prob. 73ECh. P.4 - Prob. 1QRCh. P.4 - Prob. 2QRCh. P.4 - Prob. 3QRCh. P.4 - Prob. 4QRCh. P.4 - Prob. 5QRCh. P.4 - Prob. 6QRCh. P.4 - Prob. 7QRCh. P.4 - Prob. 8QRCh. P.4 - Prob. 9QRCh. P.4 - Prob. 10QRCh. P.4 - Prob. 1ECh. P.4 - Prob. 2ECh. P.4 - Prob. 3ECh. P.4 - Prob. 4ECh. P.4 - Prob. 5ECh. P.4 - Prob. 6ECh. P.4 - Prob. 7ECh. P.4 - Prob. 8ECh. P.4 - Prob. 9ECh. P.4 - Prob. 10ECh. P.4 - Prob. 11ECh. P.4 - Prob. 12ECh. P.4 - Prob. 13ECh. P.4 - Prob. 14ECh. P.4 - Prob. 15ECh. P.4 - Prob. 16ECh. P.4 - Prob. 17ECh. P.4 - Prob. 18ECh. P.4 - Prob. 19ECh. P.4 - Prob. 20ECh. P.4 - Prob. 21ECh. P.4 - Prob. 22ECh. P.4 - Prob. 23ECh. P.4 - Prob. 24ECh. P.4 - Prob. 25ECh. P.4 - Prob. 26ECh. P.4 - Prob. 27ECh. P.4 - Prob. 28ECh. P.4 - Prob. 29ECh. P.4 - Prob. 30ECh. P.4 - Prob. 31ECh. P.4 - Prob. 32ECh. P.4 - Prob. 33ECh. P.4 - Prob. 34ECh. P.4 - Prob. 35ECh. P.4 - Prob. 36ECh. P.4 - Prob. 37ECh. P.4 - Prob. 38ECh. P.4 - Prob. 39ECh. P.4 - Prob. 40ECh. P.4 - Prob. 41ECh. P.4 - Prob. 42ECh. P.4 - Prob. 43ECh. P.4 - Prob. 44ECh. P.4 - Prob. 45ECh. P.4 - Prob. 46ECh. P.4 - Prob. 47ECh. P.4 - Prob. 48ECh. P.4 - Prob. 49ECh. P.4 - Prob. 50ECh. P.4 - Prob. 51ECh. P.4 - Prob. 52ECh. P.4 - Prob. 53ECh. P.4 - Prob. 54ECh. P.4 - Prob. 55ECh. P.4 - Prob. 56ECh. P.4 - Prob. 57ECh. P.4 - Prob. 58ECh. P.4 - Prob. 59ECh. P.4 - Prob. 60ECh. P.4 - Prob. 61ECh. P.4 - Prob. 62ECh. P.4 - Prob. 63ECh. P.4 - Prob. 64ECh. P.4 - Prob. 65ECh. P.4 - Prob. 66ECh. P.4 - Prob. 67ECh. P.4 - Prob. 68ECh. P.4 - Prob. 69ECh. P.4 - Prob. 70ECh. P.4 - Prob. 71ECh. P.5 - Prob. 1QRCh. P.5 - Prob. 2QRCh. P.5 - Prob. 3QRCh. P.5 - Prob. 4QRCh. P.5 - Prob. 5QRCh. P.5 - Prob. 6QRCh. P.5 - Prob. 7QRCh. P.5 - Prob. 8QRCh. P.5 - Prob. 9QRCh. P.5 - Prob. 10QRCh. P.5 - Prob. 1ECh. P.5 - Prob. 2ECh. P.5 - Prob. 3ECh. P.5 - Prob. 4ECh. P.5 - Prob. 5ECh. P.5 - Prob. 6ECh. P.5 - Prob. 7ECh. P.5 - Prob. 8ECh. P.5 - Prob. 9ECh. P.5 - Prob. 10ECh. P.5 - Prob. 11ECh. P.5 - Prob. 12ECh. P.5 - Prob. 13ECh. P.5 - Prob. 14ECh. P.5 - Prob. 15ECh. P.5 - Prob. 16ECh. P.5 - Prob. 17ECh. P.5 - Prob. 18ECh. P.5 - Prob. 19ECh. P.5 - Prob. 20ECh. P.5 - Prob. 21ECh. P.5 - Prob. 22ECh. P.5 - Prob. 23ECh. P.5 - Prob. 24ECh. P.5 - Prob. 25ECh. P.5 - Prob. 26ECh. P.5 - Prob. 27ECh. P.5 - Prob. 28ECh. P.5 - Prob. 29ECh. P.5 - Prob. 30ECh. P.5 - Prob. 31ECh. P.5 - Prob. 32ECh. P.5 - Prob. 33ECh. P.5 - Prob. 34ECh. P.5 - Prob. 35ECh. P.5 - Prob. 36ECh. P.5 - Prob. 37ECh. P.5 - Prob. 38ECh. P.5 - Prob. 39ECh. P.5 - Prob. 40ECh. P.5 - Prob. 41ECh. P.5 - Prob. 42ECh. P.5 - Prob. 43ECh. P.5 - Prob. 44ECh. P.5 - Prob. 45ECh. P.5 - Prob. 46ECh. P.5 - Prob. 47ECh. P.5 - Prob. 48ECh. P.5 - Prob. 49ECh. P.5 - Prob. 50ECh. P.5 - Prob. 51ECh. P.5 - Prob. 52ECh. P.5 - Prob. 53ECh. P.5 - Prob. 54ECh. P.5 - Prob. 55ECh. P.5 - Prob. 56ECh. P.5 - Prob. 57ECh. P.5 - Prob. 58ECh. P.5 - Prob. 59ECh. P.5 - Prob. 60ECh. P.5 - Prob. 61ECh. P.5 - Prob. 62ECh. P.5 - Prob. 63ECh. P.5 - Prob. 64ECh. P.5 - Prob. 65ECh. P.5 - Prob. 66ECh. P.5 - Prob. 67ECh. P.5 - Prob. 68ECh. P.5 - Prob. 69ECh. P.5 - Prob. 70ECh. P.5 - Prob. 71ECh. P.6 - Prob. 1QRCh. P.6 - Prob. 2QRCh. P.6 - Prob. 3QRCh. P.6 - Prob. 4QRCh. P.6 - Prob. 5QRCh. P.6 - Prob. 6QRCh. P.6 - Prob. 7QRCh. P.6 - Prob. 8QRCh. P.6 - Prob. 9QRCh. P.6 - Prob. 10QRCh. P.6 - Prob. 1ECh. P.6 - Prob. 2ECh. P.6 - Prob. 3ECh. P.6 - Prob. 4ECh. P.6 - Prob. 5ECh. P.6 - Prob. 6ECh. P.6 - Prob. 7ECh. P.6 - Prob. 8ECh. P.6 - Prob. 9ECh. P.6 - Prob. 10ECh. P.6 - Prob. 11ECh. P.6 - Prob. 12ECh. P.6 - Prob. 13ECh. P.6 - Prob. 14ECh. P.6 - Prob. 15ECh. P.6 - Prob. 16ECh. P.6 - Prob. 17ECh. P.6 - Prob. 18ECh. P.6 - Prob. 19ECh. P.6 - Prob. 20ECh. P.6 - Prob. 21ECh. P.6 - Prob. 22ECh. P.6 - Prob. 23ECh. P.6 - Prob. 24ECh. P.6 - Prob. 25ECh. P.6 - Prob. 26ECh. P.6 - Prob. 27ECh. P.6 - Prob. 28ECh. P.6 - Prob. 29ECh. P.6 - Prob. 30ECh. P.6 - Prob. 31ECh. P.6 - Prob. 32ECh. P.6 - Prob. 33ECh. P.6 - Prob. 34ECh. P.6 - Prob. 35ECh. P.6 - Prob. 36ECh. P.6 - Prob. 37ECh. P.6 - Prob. 38ECh. P.6 - Prob. 39ECh. P.6 - Prob. 40ECh. P.6 - Prob. 41ECh. P.6 - Prob. 42ECh. P.6 - Prob. 43ECh. P.6 - Prob. 44ECh. P.6 - Prob. 45ECh. P.6 - Prob. 46ECh. P.6 - Prob. 47ECh. P.6 - Prob. 48ECh. P.6 - Prob. 49ECh. P.6 - Prob. 50ECh. P.6 - Prob. 51ECh. P.6 - Prob. 52ECh. P.6 - Prob. 53ECh. P.6 - Prob. 54ECh. P.6 - Prob. 55ECh. P.6 - Prob. 56ECh. P.6 - Prob. 57ECh. P.7 - Prob. 1QRCh. P.7 - Prob. 2QRCh. P.7 - Prob. 3QRCh. P.7 - Prob. 4QRCh. P.7 - Prob. 5QRCh. P.7 - Prob. 6QRCh. P.7 - Prob. 7QRCh. P.7 - Prob. 8QRCh. P.7 - Prob. 9QRCh. P.7 - Prob. 10QRCh. P.7 - Prob. 1ECh. P.7 - Prob. 2ECh. P.7 - Prob. 3ECh. P.7 - Prob. 4ECh. P.7 - Prob. 5ECh. P.7 - Prob. 6ECh. P.7 - Prob. 7ECh. P.7 - Prob. 8ECh. P.7 - Prob. 9ECh. P.7 - Prob. 10ECh. P.7 - Prob. 11ECh. P.7 - Prob. 12ECh. P.7 - Prob. 13ECh. P.7 - Prob. 14ECh. P.7 - Prob. 15ECh. P.7 - Prob. 16ECh. P.7 - Prob. 17ECh. P.7 - Prob. 18ECh. P.7 - Prob. 19ECh. P.7 - Prob. 20ECh. P.7 - Prob. 21ECh. P.7 - Prob. 22ECh. P.7 - Prob. 23ECh. P.7 - Prob. 24ECh. P.7 - Prob. 25ECh. P.7 - Prob. 26ECh. P.7 - Prob. 27ECh. P.7 - Prob. 28ECh. P.7 - Prob. 29ECh. P.7 - Prob. 30ECh. P.7 - Prob. 31ECh. P.7 - Prob. 32ECh. P.7 - Prob. 33ECh. P.7 - Prob. 34ECh. P.7 - Prob. 35ECh. P.7 - Prob. 36ECh. P.7 - Prob. 37ECh. P.7 - Prob. 38ECh. P.7 - Prob. 39ECh. P.7 - Prob. 40ECh. P.7 - Prob. 41ECh. P.7 - Prob. 42ECh. P.7 - Prob. 43ECh. P.7 - Prob. 44ECh. P.7 - Prob. 45ECh. P.7 - Prob. 46ECh. P.7 - Prob. 47ECh. P.7 - Prob. 48ECh. P - Prob. 1RECh. P - Prob. 2RECh. P - Prob. 3RECh. P - Prob. 4RECh. P - In Exercises 5 and 6, simplify the expression....Ch. P - Prob. 6RECh. P - Prob. 7RECh. P - Prob. 8RECh. P - Prob. 9RECh. P - Prob. 10RECh. P - Prob. 11RECh. P - Prob. 12RECh. P - Prob. 13RECh. P - Prob. 14RECh. P - Prob. 15RECh. P - Prob. 16RECh. P - Prob. 17RECh. P - Prob. 18RECh. P - Prob. 19RECh. P - Prob. 20RECh. P - Prob. 21RECh. P - Prob. 22RECh. P - Prob. 23RECh. P - Prob. 24RECh. P - Prob. 25RECh. P - Prob. 26RECh. P - Prob. 27RECh. P - Prob. 28RECh. P - Prob. 29RECh. P - Prob. 30RECh. P - Prob. 31RECh. P - Prob. 32RECh. P - Prob. 33RECh. P - Prob. 34RECh. P - Prob. 35RECh. P - Prob. 36RECh. P - Prob. 37RECh. P - Prob. 38RECh. P - Prob. 39RECh. P - Prob. 40RECh. P - Prob. 41RECh. P - Prob. 42RECh. P - Prob. 43RECh. P - Prob. 44RECh. P - Prob. 45RECh. P - Prob. 46RECh. P - Prob. 47RECh. P - Prob. 48RECh. P - Prob. 49RECh. P - Prob. 50RECh. P - Prob. 51RECh. P - Prob. 52RECh. P - Prob. 53RECh. P - Prob. 54RECh. P - Prob. 55RECh. P - Prob. 56RECh. P - Prob. 57RECh. P - Prob. 58RECh. P - Prob. 59RECh. P - Prob. 60RECh. P - Prob. 61RECh. P - Prob. 62RECh. P - Prob. 63RECh. P - Prob. 64RECh. P - Prob. 65RECh. P - Prob. 66RECh. P - Prob. 67RECh. P - Prob. 68RECh. P - Prob. 69RECh. P - Prob. 70RECh. P - Prob. 71RECh. P - Prob. 72RECh. P - Prob. 73RECh. P - Prob. 74RECh. P - Prob. 75RECh. P - Prob. 76RECh. P - Prob. 77RECh. P - Prob. 78RECh. P - Prob. 79RECh. P - Prob. 80RECh. P - Prob. 81RECh. P - Prob. 82RECh. P - Prob. 83RE
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Quadrilaterals: Missing Angles and Sides; Author: rhornfeck;https://www.youtube.com/watch?v=knVj1O0L2TM;License: Standard YouTube License, CC-BY
STD IX | State Board | Types of Quadrilateral; Author: Robomate;https://www.youtube.com/watch?v=wh0KQ4UB0EU;License: Standard YouTube License, CC-BY