
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
4th Edition
ISBN: 9781337687805
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter H.1, Problem 69E
To determine
To show:
Expert Solution & Answer
Explanation of Solution
Given: Let point P on the curve
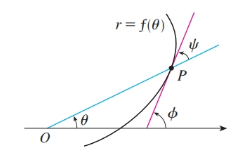
Slope of tangent,
Slope of tangent at point P on polar curve,
But
Hence proved
Chapter H.1 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Ch. H.1 - Prob. 1ECh. H.1 - Prob. 2ECh. H.1 - Prob. 3ECh. H.1 - Prob. 4ECh. H.1 - Prob. 5ECh. H.1 - Prob. 6ECh. H.1 - Prob. 7ECh. H.1 - Prob. 8ECh. H.1 - Prob. 9ECh. H.1 - Prob. 10E
Ch. H.1 - Prob. 11ECh. H.1 - Prob. 12ECh. H.1 - Prob. 13ECh. H.1 - Prob. 14ECh. H.1 - Prob. 15ECh. H.1 - Prob. 16ECh. H.1 - Prob. 17ECh. H.1 - Prob. 18ECh. H.1 - Prob. 19ECh. H.1 - Prob. 20ECh. H.1 - Prob. 21ECh. H.1 - Prob. 22ECh. H.1 - Prob. 23ECh. H.1 - Prob. 24ECh. H.1 - Prob. 25ECh. H.1 - Prob. 26ECh. H.1 - Prob. 27ECh. H.1 - Prob. 28ECh. H.1 - Prob. 29ECh. H.1 - Prob. 30ECh. H.1 - Prob. 31ECh. H.1 - Prob. 32ECh. H.1 - Prob. 33ECh. H.1 - Prob. 34ECh. H.1 - Prob. 35ECh. H.1 - Prob. 36ECh. H.1 - Prob. 37ECh. H.1 - Prob. 38ECh. H.1 - Prob. 39ECh. H.1 - Prob. 40ECh. H.1 - Prob. 41ECh. H.1 - Prob. 42ECh. H.1 - Prob. 43ECh. H.1 - Prob. 44ECh. H.1 - Prob. 45ECh. H.1 - Prob. 46ECh. H.1 - Prob. 48ECh. H.1 - Prob. 49ECh. H.1 - Prob. 50ECh. H.1 - Prob. 51ECh. H.1 - Prob. 52ECh. H.1 - Prob. 53ECh. H.1 - Prob. 54ECh. H.1 - Prob. 55ECh. H.1 - Prob. 56ECh. H.1 - Prob. 57ECh. H.1 - Prob. 58ECh. H.1 - Prob. 59ECh. H.1 - Prob. 60ECh. H.1 - Prob. 61ECh. H.1 - Prob. 62ECh. H.1 - Prob. 63ECh. H.1 - Prob. 64ECh. H.1 - Prob. 65ECh. H.1 - Prob. 66ECh. H.1 - Prob. 67ECh. H.1 - Prob. 69ECh. H.1 - Prob. 70E
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- A 20 foot ladder rests on level ground; its head (top) is against a vertical wall. The bottom of the ladder begins by being 12 feet from the wall but begins moving away at the rate of 0.1 feet per second. At what rate is the top of the ladder slipping down the wall? You may use a calculator.arrow_forwardExplain the focus and reasons for establishment of 12.4.1(root test) and 12.4.2(ratio test)arrow_forwarduse Integration by Parts to derive 12.6.1arrow_forward
- Explain the relationship between 12.3.6, (case A of 12.3.6) and 12.3.7arrow_forwardExplain the key points and reasons for the establishment of 12.3.2(integral Test)arrow_forwardUse 12.4.2 to determine whether the infinite series on the right side of equation 12.6.5, 12.6.6 and 12.6.7 converges for every real number x.arrow_forward
- use Corollary 12.6.2 and 12.6.3 to derive 12.6.4,12.6.5, 12.6.6 and 12.6.7arrow_forwardExplain the focus and reasons for establishment of 12.5.1(lim(n->infinite) and sigma of k=0 to n)arrow_forwardExplain the focus and reasons for establishment of 12.5.3 about alternating series. and explain the reason why (sigma k=1 to infinite)(-1)k+1/k = 1/1 - 1/2 + 1/3 - 1/4 + .... converges.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Fundamental Trigonometric Identities: Reciprocal, Quotient, and Pythagorean Identities; Author: Mathispower4u;https://www.youtube.com/watch?v=OmJ5fxyXrfg;License: Standard YouTube License, CC-BY