Chapter D, Problem 1RE

To determine

The coordinates of the vertex, focus and the equation of directrix.

Answer to Problem 1RE

The coordinates of the vertex is $\underset{\_}{\left(0,0\right)}$, the coordinates of focus is $\underset{\_}{\left(0,-\frac{3}{2}\right)}$ and the equation of directrix is $\underset{\_}{y=\frac{3}{2}}$.

Explanation of Solution

The given equation is $x^2=-6y$.

It is of the standard form $x^2=4py$, whose vertex is at $\left(0,0\right)$ and axis at $x=0$.

The coordinates of the focus is $\left(0,p\right)$.

Find the value of $p$.

$\begin{array}{c}p=\frac{\text{coefficient of }y}{4}\\ =\frac{-6}{4}\\ =-\frac{3}{2}\end{array}$

Therefore, the coordinates of the focus is $\left(0,-\frac{3}{2}\right)$.

Standard equation of directrix is $y=-p$.

Hence, for the given equation $x^2=-6y$, the equation of directrix is given as follows.

$\begin{array}{c}y=-p\\ =-\left(-\frac{3}{2}\right)\\ =\frac{3}{2}\end{array}$

Therefore the coordinate of the vertex is $\underset{\_}{\left(0,0\right)}$, the coordinate of focus is $\underset{\_}{\left(0,-\frac{3}{2}\right)}$ and the equation of directrix is $\underset{\_}{y=\frac{3}{2}}$.

To determine

To sketch: The parabola and its directrix for the equation $x^2=-6y$.

Explanation of Solution

Procedure used:

To sketch a parabola for an equation in the form $x^2=4py$:

1. Write the given equation in the standard form $x^2=4py$.

2. Calculate the value of $p$ from the formula,

$p=\frac{\text{coefficient of y}}{4}$

3. Plot the vertex at $\left(0,0\right)$ and focus at $\left(0,p\right)$.

4. The directrix $y=-p$ is drawn.

5. Substitute the $p$ value for $y$ in the given equation and find two points of $x$.

6. With vertex at $\left(0,0\right)$ sketch the parabola symmetric about $y-axis$.

Calculation:

The given equation is $x^2=-6y$.

From the above part $p=-\frac{3}{2}$.

Therefore, the coordinate of focus and equation of directrix are $\left(0,-\frac{3}{2}\right)$ and $\underset{\_}{y=\frac{3}{2}}$ respectively.

Substitute the value of $p=-\frac{3}{2}$ for y in the equation $x^2=-6y$.

$\begin{array}{c}{x}^2=-6y\\ =-6\left(-\frac{3}{2}\right)\\ =9\end{array}$

Taking square root on both sides.

$x=+3\text{ or }x=-3$

Therefore, the points are $\left(3,-\frac{3}{2}\right)\text{ and }\left(-3,-\frac{3}{2}\right)$.

The parabola and its directrix is sketched as follows:

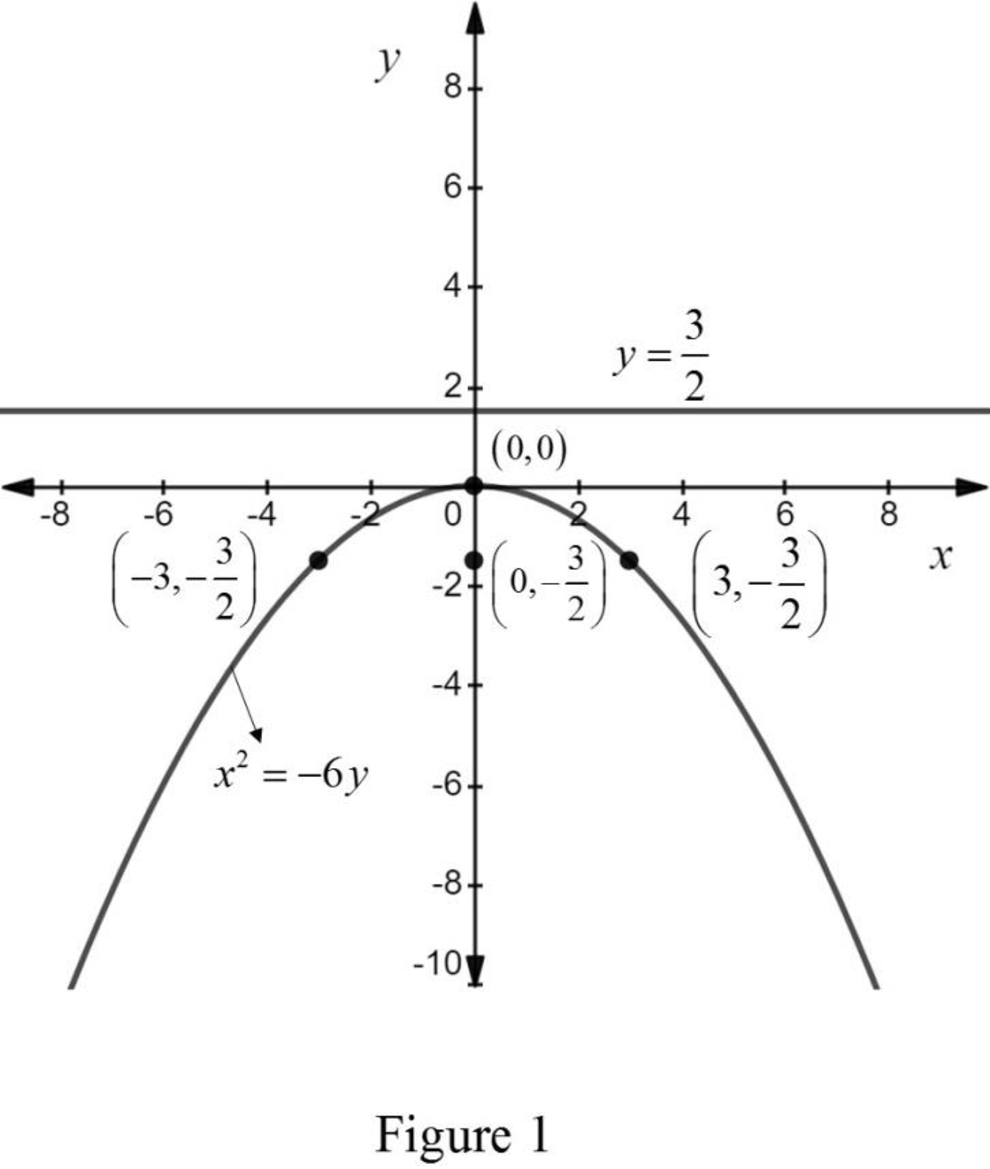
From the above graph it is observed that $y=\frac{3}{2}$ is the directrix and $\left(0,-\frac{3}{2}\right)$ is the focus.

To determine

Whether the given equation is a function or not.

Answer to Problem 1RE

The given equation $x^2=-6y$ $\underset{\_}{\text{is a function}}$.

Explanation of Solution

Procedure used:

To check whether the given equation is a function or not:

1. Plot the graph for the given equation.

2. For the resulting graph, apply the vertical line test.

3. Check whether the vertical line touches the parabola at only one point.

4. If the above condition is true, then the given equation is a function otherwise it is not a function.

Calculation:

The graph for the given equation is drawn as given below.

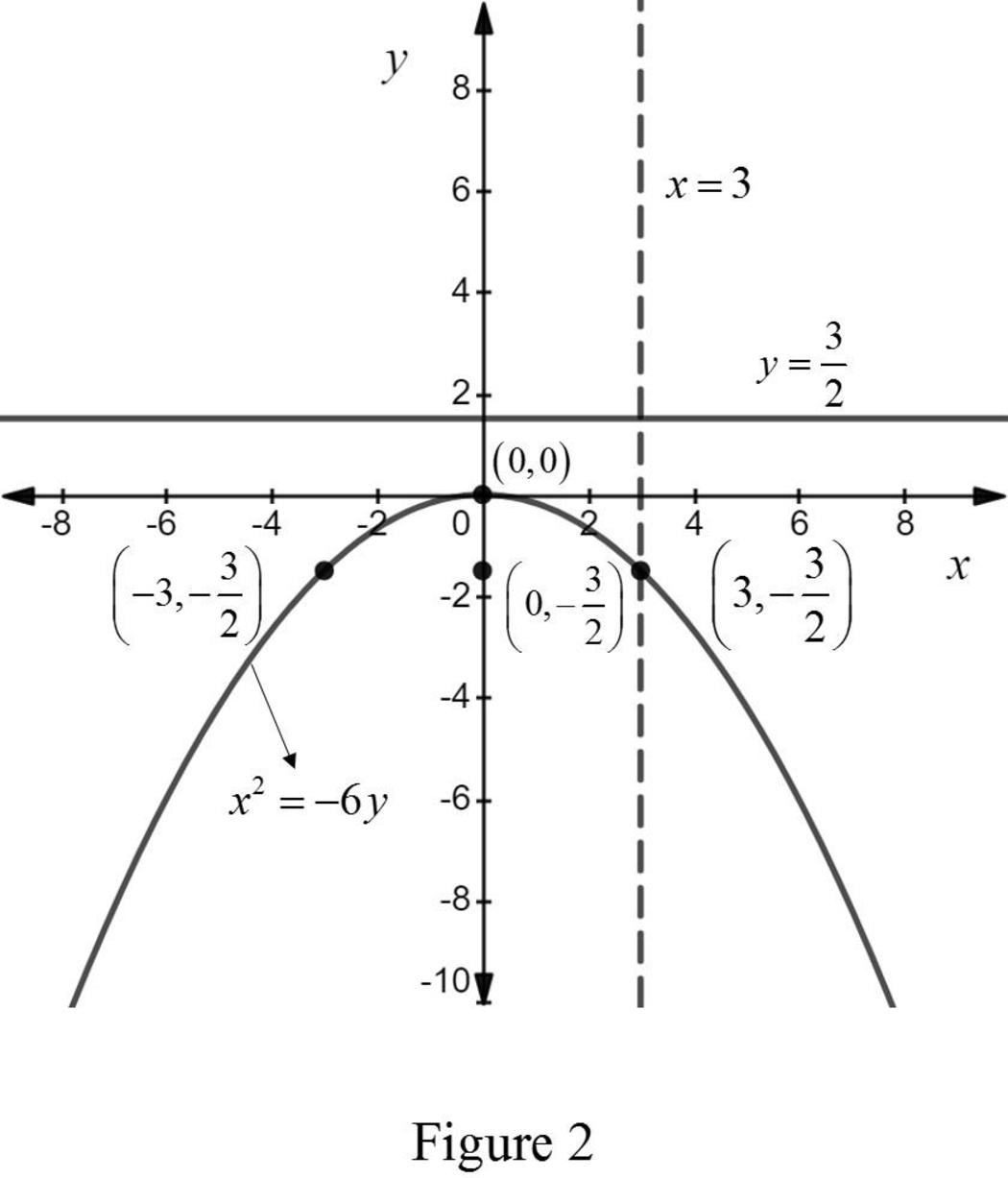
From the above figure it is observed that in the vertical line test the vertical line $x=3$ touches the parabola at only one point.

Therefore, the equation $x^2=-6y$ $\underset{\_}{\text{is a function}}$.