
a.
Explain the relationship between speed and density.
a.
Explanation of Solution
Given info:
The data related to the speed and density of traffic at the same location of a city at 10 different times within a span of 3 months.
Calculation:
Software procedure:
Step by step procedure to draw scatterplot using MINITAB software is given as,
- Choose Graph > Scatterplot.
- Choose Simple, and then click OK.
- In Y-variables, enter the column of Speed.
- In X-variables enter the column of Density.
- Click OK.
Output using MINITAB software is given as,
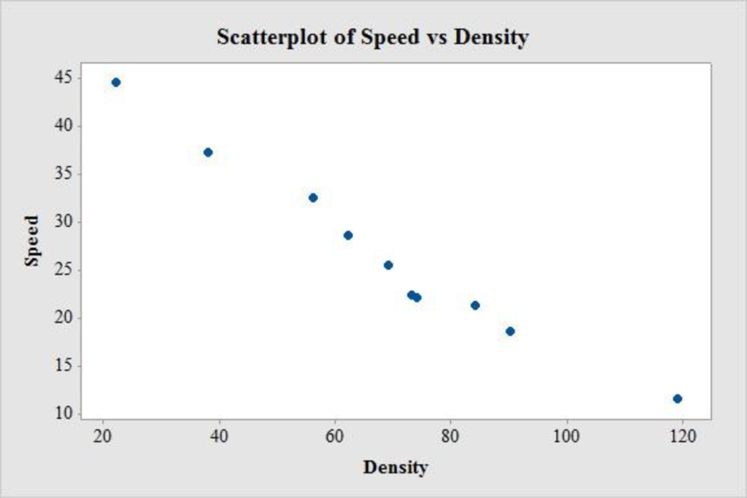
The relation between speed and density is strong, negative and linear. Thus, the association between speed and density is associated with lower speeds.
b.
Obtain a linear model to predict speed from density and comment on the appropriateness of the model.
b.
Answer to Problem 4E
The regression equation of linear model is
Explanation of Solution
Calculation:
Linear regression model:
A linear regression model is given as
Regression
Software procedure:
Step by step procedure to get the output using MINITAB software is given as,
- Choose Stat > Regression > Regression > Fit Regression Model.
- Under Responses, enter the column of Speed.
- Under predictors, enter the columns of Density.
- Click OK.
Output using MINITAB software is given below:

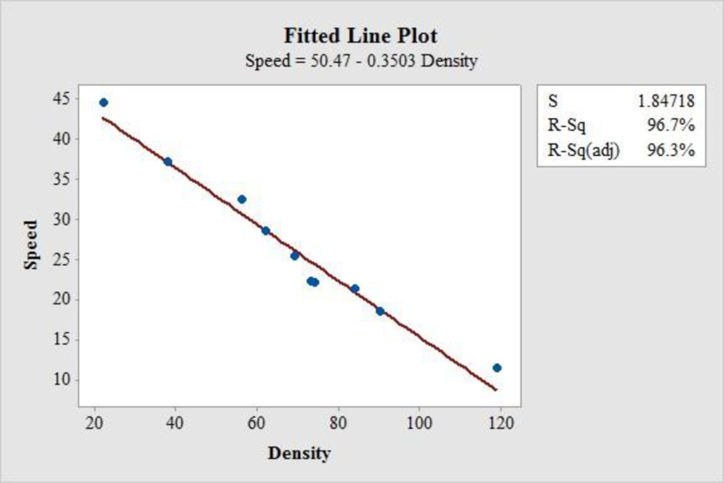
Thus, the regression equation of linear model is
The fitted scatterplot of re-expressed data exhibits a linear pattern. Thus, there is a strong and negative linear association between speed and density of traffic.
The coefficient of determination (
In the given output,
Thus, the 96.7% of the variability in speed is explained by density using linear regression model.
The conditions for a residual plot that is well fitted for the data are,
- There should not any bend, which would violate the straight line condition.
- There must not any outlier.
- There should not any change in the spread of the residuals from one part to another part of the plot.
Residual plot:
Software procedure:
Step by step procedure to get the output using MINITAB software is given as,
- Choose Stat > Regression > Regression > Fit Regression Model.
- Under Responses, enter the column of Speed.
- Under Continuous predictors, enter the columns of Density.
- In Graphs, under Residuals for plots choose Regular.
- Under Residuals plots choose Individuals plots and select box of Residuals versus fits.
- Click OK.
Output using MINITAB software is given below:
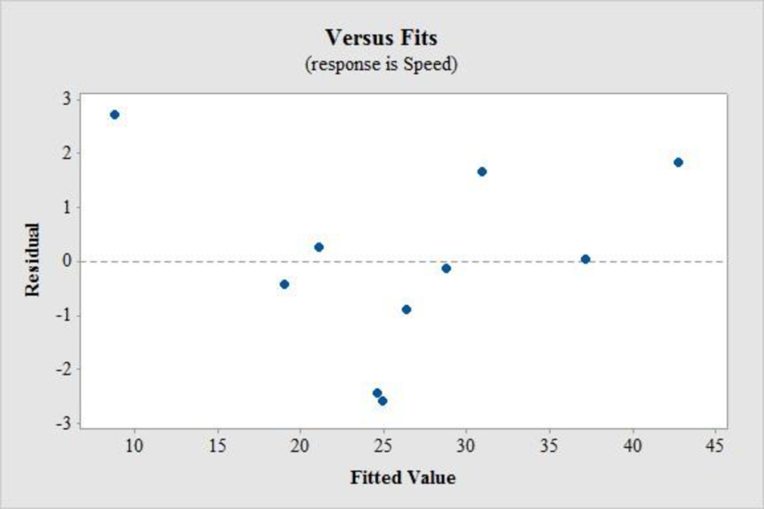
In residual plot, there is no bend or pattern, which can violate the straight line condition and there is no change in the spread of the residuals from one part to another part of the plot.
Thus, a linear model is appropriated.
c.
Find the residual of a traffic, having density and observed speed of 56 cars/mile and 32.5 mph, respectively.
Find the residual of another traffic, having density and observed speed of 20 cars/mile and 36.1 mph, respectively.
c.
Answer to Problem 4E
The residual of a traffic, having density and observed speed of 56 cars/mile and 32.5 mph, respectively is 1.65 mph and the residual of a traffic, having density and observed speed of 20 cars/mile and 36.1 mph, respectively is –7.36 mph.
Explanation of Solution
Calculation:
Assume x be the predictor variable and y be the response variable, of a
Residual:
The residual is defined as
If the observed value is less than predicted value then the residual will be negative and if the observed value is greater than predicted value then the residual will be positive.
From the previous part b. it is found that the regression equation of linear model is
The predicted speed of a traffic having density of 56 cars/mile is,
Thus, the predicted speed of a traffic having density of 56 cars/mile is 30.8532 mph.
It is known, that actual speed of a traffic having density of 56 cars/mile is 32.5 mph.
The value of the residual is,
Thus, the residual of a traffic, having density and observed speed of 56 cars/mile and 32.5 mph, respectively is 1.65 mph.
The predicted speed of a traffic having density of 20 cars/mile is,
Thus, the predicted speed of a traffic having density of 20 cars/mile is 43.46 mph.
It is known, that actual speed of a traffic having density of 20 cars/mile is 36.1 mph.
The value of the residual is,
Thus, the residual of a traffic, having density and observed speed of 20 cars/mile and 36.1 mph, respectively is –7.36 mph.
d.
Find the unusual residual.
d.
Answer to Problem 4E
Second residual is more unusual residual.
Explanation of Solution
From previous part c. it is found that residual of a traffic, having density and observed speed of 56 cars/mile and 32.5 mph, respectively is 1.65 mph and the residual of a traffic, having density and observed speed of 20 cars/mile and 36.1 mph, respectively is –7.36 mph.
Thus, it is clear that the second residual value is far away from the predicted value. Therefore, second residual is more unusual residual.
e.
Explain about slope and the
e.
Explanation of Solution
The new point
In another words, shallower slope and weaker correlation are closer to 0 as they are both started as negative quantity.
Thus, technically slope and correlation becomes higher.
f.
Predict the speed of traffic for a density of 200 cars/mile.
Explain whether the prediction is reasonable.
f.
Answer to Problem 4E
The predicted speed of a traffic having density of 200 cars/mile is –19.6 mph.
Explanation of Solution
Calculation:
The predicted speed of a traffic having density of 200 cars/mile is,
Thus, the predicted speed of a traffic having density of 200 cars/mile is –19.6 mph.
This result is not meaningful as the value of the speed comes as negative quantity, which cannot be possible. Moreover, the given car density of 200 cars/mile is far beyond from the observed values.
Thus, the prediction is not reasonable.
g.
Find the equation to predict the standardized speed from the standardized density if both the variables are standardized.
g.
Answer to Problem 4E
The equation to predict the standardized speed from the standardized density is
Explanation of Solution
Calculation:
z-score:
The z-score of a random variable x is defined as
Software Procedure:
Step by step procedure to obtain the correlation coefficient of the data using the MINITAB software:
- Choose Stat > Basic Statistics > Correlation.
- In Variables, enter the column of Speed and Density.
- Click OK in all dialogue boxes.
Output using the MINITAB software is given below:

Thus, the correlation confident for speed and density is –0.984.
It is known that, the slope
Now, for the predictor variable x and response variable y also scarify the regression equation
Consider, the mean of the predictor variable x is
Subtract the equation
Using the formula
In this problem, as speed is the predictor variable (x) and density of traffic is response variable (y) with the correlation coefficient of
h.
Find the equation to predict the standardized density from the standardized speed if both the variables are standardized.
h.
Answer to Problem 4E
The equation to predict the standardized density from the standardized speed is
Explanation of Solution
Calculation:
From the previous part g. it is found that the correlation confident for speed and density is –0.984. In addition correlation is same regardless of the direction of prediction.
Consider, the mean of the predictor variable x is
Subtract the equation
Using the formula
In this problem, as density is the predictor variable (x) and speed of traffic is response variable (y) with the correlation coefficient of
Want to see more full solutions like this?
Chapter CR Solutions
STATS:DATA+MODELS-MY LAB ACC >CUSTOM<
- Client 1 Weight before diet (pounds) Weight after diet (pounds) 128 120 2 131 123 3 140 141 4 178 170 5 121 118 6 136 136 7 118 121 8 136 127 a) Determine the mean change in patient weight from before to after the diet (after – before). What is the 95% confidence interval of this mean difference?arrow_forwardIn order to find probability, you can use this formula in Microsoft Excel: The best way to understand and solve these problems is by first drawing a bell curve and marking key points such as x, the mean, and the areas of interest. Once marked on the bell curve, figure out what calculations are needed to find the area of interest. =NORM.DIST(x, Mean, Standard Dev., TRUE). When the question mentions “greater than” you may have to subtract your answer from 1. When the question mentions “between (two values)”, you need to do separate calculation for both values and then subtract their results to get the answer. 1. Compute the probability of a value between 44.0 and 55.0. (The question requires finding probability value between 44 and 55. Solve it in 3 steps. In the first step, use the above formula and x = 44, calculate probability value. In the second step repeat the first step with the only difference that x=55. In the third step, subtract the answer of the first part from the…arrow_forwardIf a uniform distribution is defined over the interval from 6 to 10, then answer the followings: What is the mean of this uniform distribution? Show that the probability of any value between 6 and 10 is equal to 1.0 Find the probability of a value more than 7. Find the probability of a value between 7 and 9. The closing price of Schnur Sporting Goods Inc. common stock is uniformly distributed between $20 and $30 per share. What is the probability that the stock price will be: More than $27? Less than or equal to $24? The April rainfall in Flagstaff, Arizona, follows a uniform distribution between 0.5 and 3.00 inches. What is the mean amount of rainfall for the month? What is the probability of less than an inch of rain for the month? What is the probability of exactly 1.00 inch of rain? What is the probability of more than 1.50 inches of rain for the month? The best way to solve this problem is begin by creating a chart. Clearly mark the range, identifying the lower and upper…arrow_forward
- Problem 1: The mean hourly pay of an American Airlines flight attendant is normally distributed with a mean of 40 per hour and a standard deviation of 3.00 per hour. What is the probability that the hourly pay of a randomly selected flight attendant is: Between the mean and $45 per hour? More than $45 per hour? Less than $32 per hour? Problem 2: The mean of a normal probability distribution is 400 pounds. The standard deviation is 10 pounds. What is the area between 415 pounds and the mean of 400 pounds? What is the area between the mean and 395 pounds? What is the probability of randomly selecting a value less than 395 pounds? Problem 3: In New York State, the mean salary for high school teachers in 2022 was 81,410 with a standard deviation of 9,500. Only Alaska’s mean salary was higher. Assume New York’s state salaries follow a normal distribution. What percent of New York State high school teachers earn between 70,000 and 75,000? What percent of New York State high school…arrow_forwardPls help asaparrow_forwardSolve the following LP problem using the Extreme Point Theorem: Subject to: Maximize Z-6+4y 2+y≤8 2x + y ≤10 2,y20 Solve it using the graphical method. Guidelines for preparation for the teacher's questions: Understand the basics of Linear Programming (LP) 1. Know how to formulate an LP model. 2. Be able to identify decision variables, objective functions, and constraints. Be comfortable with graphical solutions 3. Know how to plot feasible regions and find extreme points. 4. Understand how constraints affect the solution space. Understand the Extreme Point Theorem 5. Know why solutions always occur at extreme points. 6. Be able to explain how optimization changes with different constraints. Think about real-world implications 7. Consider how removing or modifying constraints affects the solution. 8. Be prepared to explain why LP problems are used in business, economics, and operations research.arrow_forward
- ged the variance for group 1) Different groups of male stalk-eyed flies were raised on different diets: a high nutrient corn diet vs. a low nutrient cotton wool diet. Investigators wanted to see if diet quality influenced eye-stalk length. They obtained the following data: d Diet Sample Mean Eye-stalk Length Variance in Eye-stalk d size, n (mm) Length (mm²) Corn (group 1) 21 2.05 0.0558 Cotton (group 2) 24 1.54 0.0812 =205-1.54-05T a) Construct a 95% confidence interval for the difference in mean eye-stalk length between the two diets (e.g., use group 1 - group 2).arrow_forwardAn article in Business Week discussed the large spread between the federal funds rate and the average credit card rate. The table below is a frequency distribution of the credit card rate charged by the top 100 issuers. Credit Card Rates Credit Card Rate Frequency 18% -23% 19 17% -17.9% 16 16% -16.9% 31 15% -15.9% 26 14% -14.9% Copy Data 8 Step 1 of 2: Calculate the average credit card rate charged by the top 100 issuers based on the frequency distribution. Round your answer to two decimal places.arrow_forwardPlease could you check my answersarrow_forward
- Let Y₁, Y2,, Yy be random variables from an Exponential distribution with unknown mean 0. Let Ô be the maximum likelihood estimates for 0. The probability density function of y; is given by P(Yi; 0) = 0, yi≥ 0. The maximum likelihood estimate is given as follows: Select one: = n Σ19 1 Σ19 n-1 Σ19: n² Σ1arrow_forwardPlease could you help me answer parts d and e. Thanksarrow_forwardWhen fitting the model E[Y] = Bo+B1x1,i + B2x2; to a set of n = 25 observations, the following results were obtained using the general linear model notation: and 25 219 10232 551 XTX = 219 10232 3055 133899 133899 6725688, XTY 7361 337051 (XX)-- 0.1132 -0.0044 -0.00008 -0.0044 0.0027 -0.00004 -0.00008 -0.00004 0.00000129, Construct a multiple linear regression model Yin terms of the explanatory variables 1,i, x2,i- a) What is the value of the least squares estimate of the regression coefficient for 1,+? Give your answer correct to 3 decimal places. B1 b) Given that SSR = 5550, and SST=5784. Calculate the value of the MSg correct to 2 decimal places. c) What is the F statistics for this model correct to 2 decimal places?arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





