Chapter A.7, Problem 69E

a.

To determine

Find the times required for the triathlete to finish when she swims to different points.

Answer to Problem 69E

  $\begin{array}{lllllllll}x\hfill & 0.5\hfill & 1.0\hfill & 1.5\hfill & 2.0\hfill & 2.5\hfill & 3.0\hfill & 3.5\hfill & 4.0\hfill \\ t\hfill & 1.70\hfill & 1.72\hfill & 1.78\hfill & 1.89\hfill & 2.02\hfill & 2.18\hfill & 2.36\hfill & 2.57\hfill \end{array}$

Explanation of Solution

Given information:

An athlete has set up a course for training as part of her regimen in preparation for an upcoming triathlon. She is dropped off by a boat $2$ miles from the nearest point on shore. The finish line is $4$ miles down the coast and $2$ miles inland (see figure). She can swim $2$ miles per hour and run $6$ miles per hour. The time $t$ (in hours) required for her to reach the finish line can be approximated by the model

  $t=\frac{\sqrt{x^2+4}}{2}+\frac{\sqrt{{\left(4-x\right)}^2+4}}{6}$

Where $x$ is the distance down the coast (in miles) to the point at which she swims and then leaves the water to start her run.

  

Find the times required for the triathlete to finish when she swims to the points $x=0.5,$

  $x=1.0,\mathrm{........},x=3.5,$ and $x=4.0$ miles down the coast.

Calculation:

Here, we will consider the following model:

  $t=\frac{\sqrt{x^2+4}}{2}+\frac{\sqrt{{\left(4-x\right)}^2+4}}{6}$

Now, by using the above model we will create a table for $x=0.5,1.0,\mathrm{....},3.5,4.0$ :

  $\begin{array}{lllllllll}x\hfill & 0.5\hfill & 1.0\hfill & 1.5\hfill & 2.0\hfill & 2.5\hfill & 3.0\hfill & 3.5\hfill & 4.0\hfill \\ t\hfill & 1.70\hfill & 1.72\hfill & 1.78\hfill & 1.89\hfill & 2.02\hfill & 2.18\hfill & 2.36\hfill & 2.57\hfill \end{array}$

Hence, the result is shown in the above table.

b.

To determine

Find the distance down the coast that will yield minimum time to reach the finish line.

Answer to Problem 69E

  $\boxed{0.5}$ mile

Explanation of Solution

Given information:

An athlete has set up a course for training as part of her regimen in preparation for an upcoming triathlon. She is dropped off by a boat $2$ miles from the nearest point on shore. The finish line is $4$ miles down the coast and $2$ miles inland (see figure). She can swim $2$ miles per hour and run $6$ miles per hour. The time $t$ (in hours) required for her to reach the finish line can be approximated by the model

  $t=\frac{\sqrt{x^2+4}}{2}+\frac{\sqrt{{\left(4-x\right)}^2+4}}{6}$

Where $x$ is the distance down the coast (in miles) to the point at which she swims and then leaves the water to start her run.

  

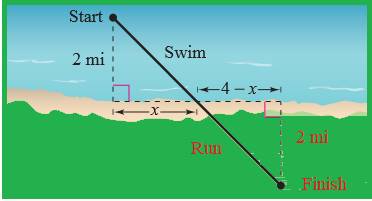
Use your results from part (a) to determine the distance down the coast that will yield the minimum amount of time required for the triathlete to reach the finish line.

Calculation:

Here, we have observed from the above table that the distance $\boxed{0.5}$ mile down the coast will yield the minimum time required for the triathlete to reach the finish line.

Hence, the result is $\boxed{0.5}$ mile.

c.

To determine

Simplify the expression.

Answer to Problem 69E

  $\boxed{\frac{3x\sqrt{x^2-8x+20}+\left(x+4\right)\sqrt{x^2+4}}{6\sqrt{x^2+4}\sqrt{x^2-8x+20}}}$

Explanation of Solution

Given information:

An athlete has set up a course for training as part of her regimen in preparation for an upcoming triathlon. She is dropped off by a boat $2$ miles from the nearest point on shore. The finish line is $4$ miles down the coast and $2$ miles inland (see figure). She can swim $2$ miles per hour and run $6$ miles per hour. The time $t$ (in hours) required for her to reach the finish line can be approximated by the model

  $t=\frac{\sqrt{x^2+4}}{2}+\frac{\sqrt{{\left(4-x\right)}^2+4}}{6}$

Where $x$ is the distance down the coast (in miles) to the point at which she swims and then leaves the water to start her run.

The expression below was obtained using calculus. It can be used to find the minimum amount of time required for the triathlete to reach the finish line. Simplify the expression.

  $\frac{1}{2}x{\left(x^2+4\right)}^{-\frac{1}{2}}+\frac{1}{6}\left(x-4\right){\left(x^2-8x+20\right)}^{-\frac{1}{2}}$

Calculation:

Here, we will consider the following equation:

  $\frac{1}{2}x{\left(x^2+4\right)}^{-\frac{1}{2}}+\frac{1}{6}\left(x-4\right){\left(x^2-8x+20\right)}^{-\frac{1}{2}}$

Now, on simplifying this equation we get:

  $\frac{1}{2}x{\left(x^2+4\right)}^{-\frac{1}{2}}+\frac{1}{6}\left(x-4\right){\left(x^2-8x+20\right)}^{-\frac{1}{2}}$

  $=\frac{x}{2\sqrt{x^2+4}}+\frac{x+4}{6\sqrt{x^2-8x+20}}$

  $=\boxed{\frac{3x\sqrt{x^2-8x+20}+\left(x+4\right)\sqrt{x^2+4}}{6\sqrt{x^2+4}\sqrt{x^2-8x+20}}}$