Chapter A5.3, Problem 39E

(a)

To determine

To find: the kind of given conic section.

Answer to Problem 39E

Here, the given curve represents a hyperbola.

Explanation of Solution

Given: $xy+2x-y=0$ and $y=-2x$ .

Calculation:

Given the following equation: $xy+2x-y=0$ .

Comparing with the standard equation for a Quadratic Curve’.

  $A{x}^2+Bxy+C{y}^2+Dx+Ey+F=0$

Thus,

  $A=0,B=1,C=0$

Now, discriminate $D$

  $\begin{array}{l}=B^2-4AC\\ ={\left(1\right)}^2-A\left(0\right)\left(0\right)\\ =1\end{array}$

Since $D>0$ , the given curve represents a hyperbola.

Conclusion:

Hence, the given curve represents a hyperbola.

(b)

To determine

To solve: the given equation and sketch the graph.

Answer to Problem 39E

Here, the given equation of curve is $y=-\frac{2x}{x-1}$ .

Explanation of Solution

Given: $xy+2x-y=0$ .

Calculation:

  $\begin{array}{l}xy+2x-y=0\\ \Rightarrow y\left(x-1\right)=-2x\\ \Rightarrow y=-\frac{2x}{x-1}\end{array}$

The graph of the above function is plotted below.

  

Conclusion:

Hence, the given equation of curve is $y=-\frac{2x}{x-1}$ .

(c)

To determine

To find: the equation for the line parallel to a line.

Answer to Problem 39E

Here, the equation for the line parallel to the line is $y=-2x-3$ .

Explanation of Solution

Given:

Line $y=-2x$ .

Calculation:

  $\begin{array}{l}y=-\frac{2x}{x-1}\\ \Rightarrow \frac{dy}{dx}=\frac{2}{{\left(x-1\right)}^2}\end{array}$

Slope of given line $y=-2x$ ,

  $m=-2$

For the lines to be normal to the curve,

  $\begin{array}{l}\frac{-1}{\frac{dy}{dx}}=m\\ \Rightarrow -\frac{{\left(x-1\right)}^2}{2}=-2\\ \Rightarrow {\left(x-1\right)}^2=4\\ \Rightarrow x=3orx=-1\end{array}$

For $x=3$ ,

  $\begin{array}{l}y=-\frac{2x}{x-1}\\ \text{ =}-\frac{2\left(3\right)}{\left(3\right)-1}\\ \text{ =}-3\end{array}$

Therefore, $\left(3,-3\right)$ is a point on the hyperbola where a line with slope $m=-2$ is normal.

So, the line is

  $y+3=-2\left(x-3\right)$

Or, $y=-2x+3$

For $x=-1$ ,

  $\begin{array}{l}y=-\frac{2x}{x-1}\\ \text{ =}-\frac{2\left(-1\right)}{\left(-1\right)-1}\\ \text{ =}-1\end{array}$

Therefore, $\left(-1,-1\right)$ is a point on the hyperbola where a line with slope $m=-2$ is normal.

So, the line is

  $y+1=-2\left(x+1\right)$

Or $y=-2x-3$

Adding the lines to the plot, the graph becomes:

  

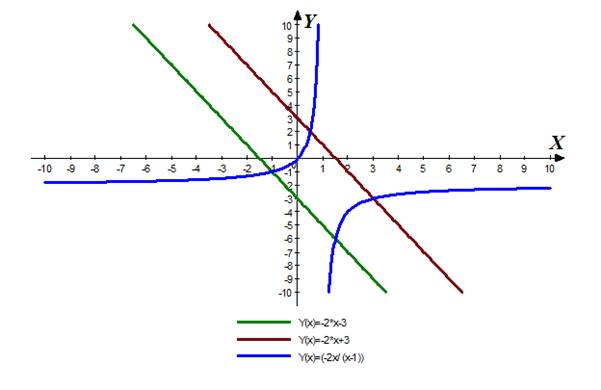
Conclusion:

Hence, the equation for the line parallel to the line is $y=-2x-3$ .