Chapter 9.R, Problem 12E

To determine

To solve:

The initial value problem $y^{\text{'}}={3x}^2{e}^y, y\left(0\right)=1$

To Graph:

The solution of the initial value problem $y^{\text{'}}={3x}^2{e}^y, y\left(0\right)=1$

Solution:

$y=-\mathrm{l}\mathrm{n}(e^{-1}-x^3)$

Explanation:

1) Concept:

The differential equation $\frac{dy}{dx}=f(x,y)$ is a variables separable differential equation if $f\left(x,y\right)=g\left(x\right)\times h\left(y\right)$

Use separation of variables for integration

Use initial point to get constant of integration.

2) Given:

The initial value problem $y^{\text{'}}={3x}^2{e}^y, y\left(0\right)=1$

3) Calculation:

$y^{\text{'}}={3x}^2{e}^y, y\left(0\right)=1$

Can be rewritten as

$e^{-y}\frac{dy}{dx} =3x^2$

$e^{-y}dy =3x^{2}dx$

By the given concept, this is a variables separable differential equation so

Integrating on both sides

$\int e^{-y}dy =\int 3x^{2}dx$

$-e^{-y}=x^3+c$

Applying initial conditions, $y\left(0\right)=1$

$c=-e^{-1}$

Therefore,

$-e^{-y}=x^3-e^{-1}$

$e^{-y}=e^{-1}{-x}^3$

Applying logarithm on both sides

$y=-\mathrm{l}\mathrm{n}(e^{-1}-x^3)$

Now to sketch of solution function, first find the domain.

Since logarithmic function is defined for positive values, we get

$e^{-1}-x^3>0 \Rightarrow x^3<e^{-1} \Rightarrow x<e^{-\frac{1}{3}}\approx 0.72$

So the domain is $\left(-\infty , e^{-\frac{1}{3}}\right)$ and using graphing calculator, graph is as below

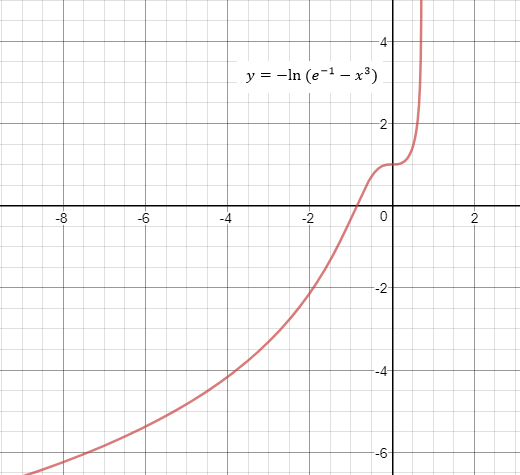
Conclusion:

The solution of the initial value problem $y^{\text{'}}={3x}^2{e}^y, y\left(0\right)=1 is$ $y=-\mathrm{l}\mathrm{n}(e^{-1}-x^3)$

And sketch of solution function is given below.