Elementary Geometry for College Students
6th Edition
ISBN: 9781285195698
Author: Daniel C. Alexander, Geralyn M. Koeberlein
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 9.CT, Problem 1CT
For the regular pentagonal prism shown below, find the total number of
| a) edges. ______ | b) faces. _______ |
 |
 |
Expert Solution
To determine
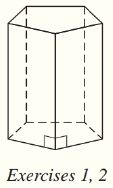a)
To find:
The total number of edges for the regular pentagon prism.
Answer to Problem 1CT
Solution:
The total number of edges in the regular pentagon prism is 15.
Explanation of Solution
Given:
The regular pentagon prism is shown below.’
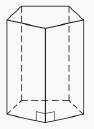
Calculation:
We see that the base of the regular pentagon prism is a regular pentagon.
We know that there are five edges in a regular pentagon.
Therefore one base of the regular pentagon prism has five edges.
Since there are two bases, there are 10 base edges.
Also, there are five lateral edges.
Thus the number of edges in the regular pentagon prism is
Final statement:
Therefore the total number of edges in the regular pentagon prism is 15.
Expert Solution
To determine
b)
To find:
The total number of faces for the regular pentagon prism.
Answer to Problem 1CT
Solution:
The total number of faces in the regular pentagon prism is 7.
Explanation of Solution
Given:
The regular pentagon prism is shown below.’
Calculation:
We see that there are two base faces and five lateral faces.
Hence the total number of faces is 7.
Final statement:
Therefore the total number of faces in the regular pentagon prism is 7.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
1) Given: MNPQ is a parallelogram with MP 1 NQ.
Prove: MNPQ is a rhombus.
Statement
M
Reason
Q
R
1) Given: MNPQ is a parallelogram with MP 1 NQ.
Prove: MNPQ is a rhombus.
Statement
Reason
M
R
P
4) Find a proposition with three variables p, q, and r that is never true.
5) Determine whether this proposition is a tautology using propositional
equivalence and laws of logic: ((p
(bv (bL ←
→¬p
[1
6) Explain why the negation of "Some students in my class use e-mail” is not "Some
students in my class do not use e-mail".
Chapter 9 Solutions
Elementary Geometry for College Students
Ch. 9.1 - Consider the solid shown. a Does it appear to be a...Ch. 9.1 - Consider the solid shown. a Does it appear to be a...Ch. 9.1 - Consider the hexagonal prism shown in Exercise 1....Ch. 9.1 - Consider the triangular prism shown in Exercise 2....Ch. 9.1 - If each edge of the hexagonal prism in Exercise 1...Ch. 9.1 - If each edge of the triangular prism in Exercise...Ch. 9.1 - Suppose that each of the bases of the hexagonal...Ch. 9.1 - Suppose that each of the bases of the triangular...Ch. 9.1 - Suppose that each of bases of the hexagonal prism...Ch. 9.1 - Suppose that each of the bases of the triangular...
Ch. 9.1 - A solid is an octagonal prism. a How many vertices...Ch. 9.1 - A solid is a pentagonal prism. a How many vertices...Ch. 9.1 - Generalize the results found in Exercise 11 and 12...Ch. 9.1 - In the accompanying regular pentagonal prism,...Ch. 9.1 - In the regular pentagonal prism shown above,...Ch. 9.1 - For the right triangular prism, suppose that the...Ch. 9.1 - For the right triangular prism found in Exercise...Ch. 9.1 - Prob. 18ECh. 9.1 - Given that 12 in. =1 ft, find the number of cubic...Ch. 9.1 - Find the volume and the surface area of a closed...Ch. 9.1 - Find the volume and the surface area of a closed...Ch. 9.1 - A cereal box measures 2 in. by 8 in. by 10 in....Ch. 9.1 - The measures of the sides of the square base of a...Ch. 9.1 - For a given box, the height measures 4 m. If the...Ch. 9.1 - For the box shown, the total area is 94 cm2....Ch. 9.1 - If the volume of the box is 252 in3, find the...Ch. 9.1 - The box with dimensions indicated is to be...Ch. 9.1 - A hollow steel door is 32 in. wide by 80 in. tall...Ch. 9.1 - A storage shed is in the shape of a pentagonal...Ch. 9.1 - A storage shed is in the shape of a trapezoidal...Ch. 9.1 - Prob. 31ECh. 9.1 - Prob. 32ECh. 9.1 - When the length of each edge of a cube is...Ch. 9.1 - The numerical value of the volume of a cube equals...Ch. 9.1 - The sum of the lengths of all edges of a cube is...Ch. 9.1 - Prob. 36ECh. 9.1 - Zaidah plans a raised flower bed 2 ft high by 12...Ch. 9.1 - In excavating for a new house, a contractor digs a...Ch. 9.1 - Kristine creates an open box by cutting congruent...Ch. 9.1 - As in Exercise 39, find the volume of the box if...Ch. 9.1 - Kiannas aquarium is box-shaped with dimensions of...Ch. 9.1 - The gasoline tank on an automobile is box-shaped...Ch. 9.1 - Prob. 43ECh. 9.1 - Prob. 44ECh. 9.1 - For Exercise 43 to 45, consider the oblique...Ch. 9.1 - It can be shown that the length of a diagonal of a...Ch. 9.1 - A diagonal of a cube joins two vertices so that...Ch. 9.2 - Prob. 1ECh. 9.2 - Prob. 2ECh. 9.2 - Prob. 3ECh. 9.2 - Prob. 4ECh. 9.2 - Prob. 5ECh. 9.2 - Prob. 6ECh. 9.2 - Prob. 7ECh. 9.2 - Prob. 8ECh. 9.2 - Prob. 9ECh. 9.2 - Prob. 10ECh. 9.2 - Prob. 11ECh. 9.2 - Prob. 12ECh. 9.2 - Prob. 13ECh. 9.2 - Refer to the prisms of Exercises 1 and 2. Which of...Ch. 9.2 - Prob. 15ECh. 9.2 - Refer to the prisms of Exercises 1 and 2. Which of...Ch. 9.2 - Prob. 17ECh. 9.2 - Prob. 18ECh. 9.2 - Prob. 19ECh. 9.2 - Prob. 20ECh. 9.2 - Prob. 21ECh. 9.2 - Prob. 22ECh. 9.2 - Prob. 23ECh. 9.2 - Prob. 24ECh. 9.2 - Prob. 25ECh. 9.2 - Prob. 26ECh. 9.2 - Prob. 27ECh. 9.2 - Prob. 28ECh. 9.2 - Prob. 29ECh. 9.2 - Before the shingles of the steeple see Exercise 29...Ch. 9.2 - Prob. 31ECh. 9.2 - Prob. 32ECh. 9.2 - Prob. 33ECh. 9.2 - Prob. 34ECh. 9.2 - Prob. 35ECh. 9.2 - Prob. 36ECh. 9.2 - Prob. 37ECh. 9.2 - Prob. 38ECh. 9.2 - Prob. 39ECh. 9.2 - Prob. 40ECh. 9.2 - Prob. 41ECh. 9.2 - Prob. 42ECh. 9.2 - Prob. 43ECh. 9.2 - Prob. 44ECh. 9.2 - Prob. 45ECh. 9.3 - Does a right circular cylinder such as an aluminum...Ch. 9.3 - Does a right circular cone such as a wizards cap...Ch. 9.3 - Prob. 3ECh. 9.3 - For the right circular cylinder shown on page 417,...Ch. 9.3 - For the right circular cylinder, suppose that r=5...Ch. 9.3 - Suppose that r=12 cm and h=15 cm in the right...Ch. 9.3 - The tin can shown at the right has the indicated...Ch. 9.3 - Prob. 8ECh. 9.3 - If the exact volume of a right circular cylinder...Ch. 9.3 - Suppose that the volume of an aluminum can is to...Ch. 9.3 - For an aluminum can, the lateral surface area is...Ch. 9.3 - Find the height of a storage tank in the shape of...Ch. 9.3 - Find the volume of the oblique circular cylinder....Ch. 9.3 - A cylindrical orange juice container has metal...Ch. 9.3 - Prob. 15ECh. 9.3 - In Exercises 15 to 20, use that fact that r2+h2=l2...Ch. 9.3 - Prob. 17ECh. 9.3 - In Exercises 15 to 20, use that fact that r2+h2=l2...Ch. 9.3 - Prob. 19ECh. 9.3 - Prob. 20ECh. 9.3 - The oblique circular cone has an altitude and a...Ch. 9.3 - For the accompanying right circular cone, h=6 m...Ch. 9.3 - Prob. 23ECh. 9.3 - Rukia discovers that the teepee with a circular...Ch. 9.3 - Prob. 25ECh. 9.3 - Prob. 26ECh. 9.3 - Prob. 27ECh. 9.3 - A triangle has sides that measure 15 cm, 20 cm,...Ch. 9.3 - Prob. 29ECh. 9.3 - Prob. 30ECh. 9.3 - If a right circular cone has a circular base with...Ch. 9.3 - A right circular cone has a slant height of 12 ft...Ch. 9.3 - A solid is formed by cutting a conical section...Ch. 9.3 - Prob. 34ECh. 9.3 - In Exercises 34 and 35, give a paragraph proof for...Ch. 9.3 - For a right circular cone, the slant height has a...Ch. 9.3 - For a right circular cone, the ratio of the slant...Ch. 9.3 - If the length of the radius and the height of a...Ch. 9.3 - Prob. 39ECh. 9.3 - For a right circular cone, the dimensions are r=6...Ch. 9.3 - A cylindrical storage tank has a depth of 5 ft and...Ch. 9.3 - Prob. 42ECh. 9.3 - A frustum of a cone is the portion of the cone...Ch. 9.3 - In Exercises 44 and 45, use the formula from...Ch. 9.3 - In Exercises 44 and 45, use the formula from...Ch. 9.3 - Prob. 46ECh. 9.3 - Prob. 47ECh. 9.3 - Prob. 48ECh. 9.3 - A lawn roller in the shape of a right circular...Ch. 9.4 - Which of these two polyhedrons is concave? Note...Ch. 9.4 - For Figure a of Exercise 1, find the number of...Ch. 9.4 - Prob. 3ECh. 9.4 - For a regular tetrahedron, find the number of...Ch. 9.4 - For a regular hexahedron, find the number of...Ch. 9.4 - A regular polyhedron has 12 edges and 8 vertices....Ch. 9.4 - A regular polyhedron has 12 edges and 6 vertices....Ch. 9.4 - A polyhedron not regular has 10 vertices and 7...Ch. 9.4 - A polyhedron not regular has 14 vertices and 21...Ch. 9.4 - Prob. 10ECh. 9.4 - Prob. 11ECh. 9.4 - Prob. 12ECh. 9.4 - In sphere O, the length of radius OP- is 6 in....Ch. 9.4 - Find the approximate surface area and volume of...Ch. 9.4 - Find the total area surface area of a regular...Ch. 9.4 - Find the total area surface area of a regular...Ch. 9.4 - Find the total area surface area of a regular...Ch. 9.4 - Prob. 18ECh. 9.4 - Prob. 19ECh. 9.4 - Prob. 20ECh. 9.4 - Find the approximate volume of a sphere with...Ch. 9.4 - Prob. 22ECh. 9.4 - The surface of a soccer ball is composed of 12...Ch. 9.4 - A calendar is determined by using each of the 12...Ch. 9.4 - A sphere is inscribed within a right circular...Ch. 9.4 - In calculus, it can be shown that the largest...Ch. 9.4 - Given that a regular polyhedron of n faces is...Ch. 9.4 - A right circular cone is inscribed in a sphere. If...Ch. 9.4 - A sphere is inscribed in a right circular cone...Ch. 9.4 - In Exercises 31 and 32, use the calculator value...Ch. 9.4 - Prob. 32ECh. 9.4 - A sphere has a volume equal to 997in3. Determine...Ch. 9.4 - Prob. 34ECh. 9.4 - The spherical storage tank described in Example 5...Ch. 9.4 - An observatory has the shape of a right circular...Ch. 9.4 - A leather soccer ball has an inside diameter...Ch. 9.4 - An ice cream cone is filled with ice cream as...Ch. 9.4 - For Exercises 39 to 44, make drawings as needed....Ch. 9.4 - For Exercises 39 to 44, make drawings as needed....Ch. 9.4 - For Exercises 39 to 44, make drawings as needed....Ch. 9.4 - For Exercises 39 to 44, make drawings as needed....Ch. 9.4 - For Exercises 39 to 44, make drawings as needed....Ch. 9.4 - For Exercises 39 to 44, make drawings as needed....Ch. 9.4 - Prob. 45ECh. 9.4 - Suppose that a semicircular region with vertical...Ch. 9.4 - Prob. 47ECh. 9.4 - Sketch the solid that results when the given...Ch. 9.4 - Explain how the following formula used in Example...Ch. 9.4 - Prob. 50ECh. 9.CR - Each side of the base of a right octagonal prism...Ch. 9.CR - The base of a right prism is a triangle whose...Ch. 9.CR - The height of a square box is 2 in. more than...Ch. 9.CR - Prob. 4CRCh. 9.CR - The base of a right prism is a triangle whose...Ch. 9.CR - The base of a right prism is a regular hexagon...Ch. 9.CR - Prob. 7CRCh. 9.CR - Prob. 8CRCh. 9.CR - Prob. 9CRCh. 9.CR - The diameter of the base of a right circular cone...Ch. 9.CR - Prob. 11CRCh. 9.CR - Prob. 12CRCh. 9.CR - The radius length of the base of a right circular...Ch. 9.CR - a For the through in the shape of half-cylinder,...Ch. 9.CR - The slant height of a right circular cone is 12...Ch. 9.CR - The volume of the right circular cone is 96 in. If...Ch. 9.CR - Find the surface area of a sphere if the radius...Ch. 9.CR - Find the volume of a sphere if the diameter has...Ch. 9.CR - The solid shown consists of a hemisphere half of a...Ch. 9.CR - If the radius length of one sphere is three times...Ch. 9.CR - Find the volume of the solid of revolution that...Ch. 9.CR - Prob. 22CRCh. 9.CR - Find the exact volume of the solid of revolution...Ch. 9.CR - A plastic pipe is 3 ft long and has an inside...Ch. 9.CR - Prob. 25CRCh. 9.CR - Prob. 26CRCh. 9.CR - A drug manufacturing company wants to manufacture...Ch. 9.CR - Prob. 28CRCh. 9.CR - Find the volume of cement used in the block shows.Ch. 9.CR - Given a die in the shape of a regular octahedron,...Ch. 9.CR - Find the total surface area of a a regular...Ch. 9.CR - Three spheres are externally tangent to each other...Ch. 9.CT - For the regular pentagonal prism shown below, find...Ch. 9.CT - Prob. 2CTCh. 9.CT - Prob. 3CTCh. 9.CT - For the regular square pyramid shown above, find a...Ch. 9.CT - Prob. 5CTCh. 9.CT - Prob. 6CTCh. 9.CT - Prob. 7CTCh. 9.CT - Determine whether the statement is true or false....Ch. 9.CT - Determine whether the statement is true or false....Ch. 9.CT - Prob. 10CTCh. 9.CT - Prob. 11CTCh. 9.CT - Prob. 12CTCh. 9.CT - The exact volume of a right circular cone not...Ch. 9.CT - Assume that a die used for gaming is in the shape...Ch. 9.CT - A spherical storage tank filled with water has a...Ch. 9.CT - Prob. 16CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Milgram lemma B) Consider Show that -Au= f in a u=0 on on llu-ulls Chllullz 02 Prove that Where ||ul| = a(u, u) = vu. Vu dx + fonu.u ds Q3: Let V = H' (2), a(u,v) = CR, a(u,v) = (f,v) where Vu. Vv dx + Ja cuv dx and ||u|=|||| Show that a(u, v) is V-ellipiticly and continuity.arrow_forward7) Is the following statement True or False: AU BUA = Ā. Justify your answer. 8) Suppose g: A → B and f: B → C where A = {2,3,6,8}, and g and f are defined by g = {a, b, c, d}, B = {1,2,3}, C = {(a,2), (b,1), (c, 3), (d, 2)} and f = {(1,8),(2,3), (3,2)}. Find fog, gof and f−¹. 9) Verify that a₁ = 7(3") -π is a solution to the recurrence relation an = an 4an-1 -3an-2arrow_forward1) Find the prime factorization of 111111. 2) Find (-88 mod 13) 5 mod 7. 3) Use the Euclidean algorithm to find gcd(144,233).arrow_forward
- 3 10) Suppose B = 2 4 5) and C = (b 2 prove that no such matrix exists. (6 1) . Find a matrix A such that AB = C orarrow_forwardi let V-H.) R aluv) = (v) where alu)=SU. V dx and { and (v) sv Show that the finite element solution Un Unique Prove that U-Un ll≤ch llull A²=f and U= Ju =0 on on a with bili near from a (u,v) = SAU. Av dr 32 Prove that aluv) is countinous and V-expitic ii Prove that 2 Mete ||(U-U|| ²== ||||²+|| || ² where -Auf in U=0 on 2arrow_forwardConcdsider the following problem in R² ди -MAU+B+P+4= f inv ax U= 0 of 2 Bi-1, 2 are so prove. that al) is continous and, V-elliptic ⑥Provethat 14-Ull, s chllull zudx Where lull" = a(u,u) = £14. Ju 2 dx+ u.uds an let U= x(1-x)y (1-y) is gol. to -Au=f Compute || Ull Li and lull in are Ju, Duarrow_forward
- Make Varitional for Malation for Problem and prove al.,.) is continous and, V-elliptic 224 2x² - -40² 4+24=1 ayz Xe=oonT 1 - €4 +x4 +4 = f XE I = (0,2), 4(a)=(()=0 (iii) - Au+S4=f Xen yo U=0, XE INarrow_forward4) Given: LMNP is a parallelogram, PRSM, LR 1 PM, and NS 1 PM Prove: PS MR Statement Reason P L S R N Marrow_forward5) Given: Quadrilateral MNPQ with Fill in the missing reasons to show MNPQ is a parallelogram. 1/4 and 2 = 3. M N 1 2 4 3 Reason P Statement 1. 1 ≈ 4 and 2 = <3 1. Given 2. NQ=NQ 2. 3. AMNQ = APQN 3. 4. MN QP and NP = MQ 4. 5. MNPQ is a parallelogram 5.arrow_forward
- 3) Given: EFGH is a parallelogram and ZH is a right angle. Prove: EFGH is a rectangle. E F G Harrow_forwardDirections: In parallelogram QRST shown, mZQRS = 61°, mZQST = 52°, and point U is located on QR such that TU is perpendicular to diagonal QS. (a) Determine the measure of TQR. (b) Determine the measure of /TQS. (c) Determine the measure of ZQTU. U R Sarrow_forwardonsider the variational form a(u,v) = (f,v) where a(u,v) = 'u'v' dx Prove that VvE H(0, 1), i = 1, 2,...., n - 1 a(v,q)=-v(x-1) + 2v(x) = v(x+1)] h - where (,), CV, is usual basis of hat functions Q2: A: Consider the problem A²u = f and u= ди On = 0 on an With bilinear form a(u,v) = f Au. Av dn prove that a(u,v) V-ellpitic. B: Prove that Where lu-ulls Chulz lul = a(u, u) = f vu.vu dx + fonu. uds Q3: Consider the problem -V. (Vu) + u = 0, in n.Vu=gN on an 1- Show that the solution u of the problem satisfies the stability lulul≤ Clignlin (use 2abarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
What is a Prism? | Types of Prism | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=wxDTrgnyu28;License: Standard YouTube License, CC-BY