Chapter 9.7, Problem 60AYU

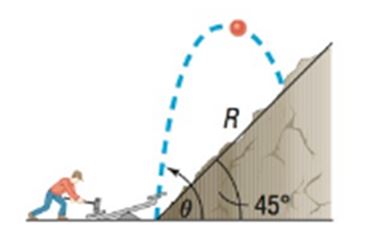
Projectile Motion The position of a projectile fired with an initial velocity ${\upsilon }_0$ feet per second and at an angle $\theta$ to the horizontal at the end of $t$ seconds is given by the parametric equations

$x=\left({\upsilon }_0\cos \theta \right)t$ $y=\left({\upsilon }_0\sin \theta \right)t-16t^2$

See the illustration.

a. Obtain the rectangular equation of the trajectory and identify the curve.

b. Show that the projectile hits the ground $\left(y=0\right)$ when $t=\frac{1}{16}{\upsilon }_0\sin \theta$.

c. How far has the projectile traveled (horizontally) when it strikes the ground? In other words, find the range $R$.

d. Find the time $t$ when $x=y$. Then find the horizontal distance $x$ and the vertical distance $y$ traveled by the projectile in this time. Then compute $\sqrt{x^2+y^2}$. This is the distance $R$, the range, that the projectile travels up a plane inclined at ${45}^{\circ }$ to the horizontal $\left(x=y\right)$. See the following illustration. (See also Problem 99 in Section 7.6.)