
Concept explainers
For the beam and loading shown, determine (a) the slope at point B, (b) the deflection at point D. Use E = 200 GPa.

Fig. P9.128
The magnitude
Answer to Problem 146P
The magnitude
Explanation of Solution
Given information:
The section of the beam is
The young’s modulus of steel is
Calculation:
Show the free body diagram of the beam as in Figure 1.
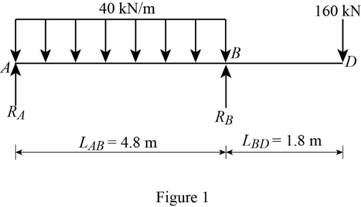
Calculate the vertical reaction at point A by taking moment about point B.
Refer Appendix C “Properties of rolled steel shape (SI units)” for moment of inertia of section
Calculate the value (EI):
Substitute
Calculate the moment due to the reaction at A:
Substitute
Calculate the
Substitute
Show the
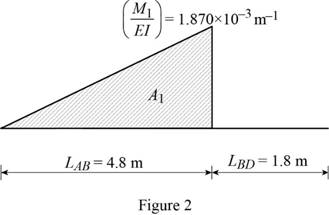
Calculate the area
Substitute
Calculate the moment due UDL:
Substitute
Calculate the
Substitute
Show the
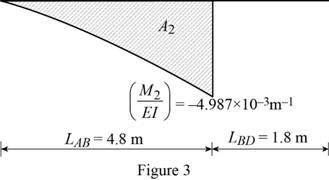
Calculate the area
Substitute
Calculate the moment due to the point load at D as below:
Substitute
Calculate the
Substitute
Show the
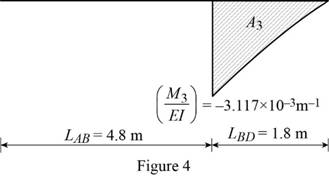
Calculate the area
Substitute
Calculate the tangential deviation of B with respect to A using the relation:
Substitute
Calculate the slope
Substitute
Let point K is the maximum deflection.
Calculate the moment due to the reaction at A as below:
Substitute
Calculate the
Substitute
Calculate the moment due UDL:
Calculate the
Substitute
Show the
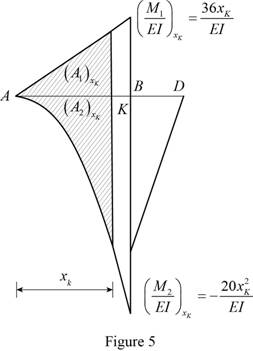
Calculate the area
Substitute
Calculate the area
Substitute
Calculate the slope
Substitute
Differentiate the Equation (1).
Solve the value
Iteration 1:
Substitute 3 for
Substitute 3 for
Iteration 2:
Calculate the value
Substitute 3 for
Similarly calculate the value
| f | ||
| 3 | 28.08 | -72 |
| 3.39 | -6.78 | -107.8 |
| 3.327 | -0.188 | -101.6 |
| 3.3251 | 0.005 | -101.42 |
| 3.32514 | 0.0001 |
The value of
Calculate the slope at the end A related to the point K
Substitute
Calculate the magnitude
Substitute
Thus, the magnitude
Want to see more full solutions like this?
Chapter 9 Solutions
EBK MECHANICS OF MATERIALS
- aversity of Baoyion aculty of Engineering-AIMusyab Automobile Eng. Dep. Year: 2022-2023, st Course, 1st Attempt Stage: 3rd Subject: Heat Transfer I Date: 2023\01\23- Monday Time: 3 Hours Q4: A thick slab of copper initially at a uniform temperature of 20°C is suddenly exposed to radiation at one surface such that the net heat flux is maintained at a constant value of 3×105 W/m². Using the explicit finite-difference techniques with a space increment of Ax = = 75 mm, determine the temperature at the irradiated surface and at an interior point that is 150 mm from the surface after 2 min have elapsed. Q5: (12.5 M) A) A steel bar 2.5 cm square and 7.5 cm long is initially at a temperature of 250°C. It is immersed in a tank of oil maintained at 30°C. The heat-transfer coefficient is 570 W/m². C. Calculate the temperature in the center of the bar after 3 min. B) Air at 90°C and atmospheric pressure flows over a horizontal flat plate at 60 m/s. The plate is 60 cm square and is maintained at a…arrow_forwardUniversity of Baby on Faculty of Engineering-AIMusyab Automobile Eng. Dep. Year: 2022-2023. 1 Course, 1" Attempt Stage 3 Subject Heat Transfer I Date: 2023 01 23- Monday Time: 3 Hours Notes: Q1: • • Answer four questions only Use Troles and Appendices A) A flat wall is exposed to an environmental temperature of 38°C. The wall is covered with a layer of insulation 2.5 cm thick whose thermal conductivity is 1.4 W/m. C, and the temperature of the wall on the inside of the insulation is 315°C. The wall loses heat to the environment by convection. Compute the value of the convection heat-transfer coefficient that must be maintained on the outer surface of the insulation to ensure that the outer-surface temperature does not exceed 41°C. B) A vertical square plate, 30 cm on a side, is maintained at 50°C and exposed to room air at 20°C. The surface emissivity is 0.8. Calculate the total heat lost by both sides of the plate. (12.5 M) Q2: An aluminum fin 1.5 mm thick is placed on a circular tube…arrow_forwardSolve using graphical method and analytical method, only expert should solvearrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





