
Concept explainers
Water is being poured at a steady rate into a round vase whose vertical cross-section is shown in Figure 9.63 . One function that arises from this situation is the volume function, whose input is the time elapsed since water began pouring into the vase and whose output is the volume of water in the vase at that time. Another function that arises from this situation is the height function, whose input is the time elapsed since water began pouring into the vase and whose, output is theheight of the water in the vase at that time. Sketch graphs that could be the graphs of these two functions, and indicate how the graphs fit with the scnario of water pouringinto th vase at the steady rate .
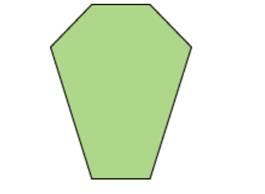
Figure 9.63 the cross section of the vase
Want to see the full answer?
Check out a sample textbook solution
Chapter 9 Solutions
Mathematics for Elementary Teachers with Activities Plus MyLab Math -- Title-Specific Access Card Package (5th Edition)
Additional Math Textbook Solutions
Pathways To Math Literacy (looseleaf)
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Introductory Statistics
University Calculus: Early Transcendentals (4th Edition)
- Let {Yt} be an AR(2) process of the special form Yt = φ2Yt − 2 + et. Use first principles to find the range of values of φ2 for which the process is stationary.arrow_forwardDescribe the important characteristics of the autocorrelation function for the following models: (a) MA(1), (b) MA(2), (c) AR(1), (d) AR(2), and (e) ARMA(1,1).arrow_forwarda) prove that if (x) is increasing then (x~) is bounded below and prove if (is decrasing then (xn) is bounded above- 6) If Xn is bounded and monotone then (Xa) is Convergent. In particular. i) if (xn) is bounded above and incrasing then lim xn = sups xn: ne№3 n700 ii) if (X) is bounded below and decrasing then I'm Xn = inf\x₂,neN} 4500 143arrow_forward
- 5. Consider the following vectors 0.1 3.2 -0-0-0 = 5.4 6.0 = z= 3 0.1 For each of exercises a-e, either compute the desired quantity by hand with work shown or explain why the desired quantity is not defined. (a) 10x (b) 10-27 (c) J+Z (d) (x, y) (e) (x, z)arrow_forward1) let X: N R be a sequence and let Y: N+R be the squence obtained from x by di scarding the first meN terms of x in other words Y(n) = x(m+h) then X converges to L If and only is y converges to L- 11) let Xn = cos(n) where nyo prove D2-1 that lim xn = 0 by def. h→00 ii) prove that for any irrational numbers ther exsist asquence of rational numbers (xn) converg to S.arrow_forwardConsider the graph/network plotted below. 1 6 5 3 Explicitly give (i.e., write down all of the entries) the adjacency matrix A of the graph.arrow_forward
- . Given the function f: XY (with X and Y as above) defined as f(2) = 2, f(4) = 1, ƒ(6)=3, ƒ(8) = 2, answer the following questions. Justify your answers. (a) [4 points] Is f injective? (b) [4 points] Is f surjective? (c) [2 points] Is f bijective?arrow_forward1. Let 15 -14 A = -10 9 13-12 -8 7 11 15 -14 13 -12 -6 and B = -10 9 -8 7 -6 5 -4 3 -2 E 5 -4 3 -2 1 Explicitly give the values of A2,3, A1,5, and B1,4- Is A a 5 x 3 matrix? Explain your answer. Are A and B (mathematically) equal? Explain your answer.arrow_forwardGiven the following set X = {2, 4, 6, 8} and Y = {1, 2, 3}, explicitly give (e.g., write down the sets with numerical entries) of the outputs of the following requested set operations: (a) [2 points] XUY (Union) (b) [2 points] XY (Intersection) (c) [3 points] X\Y (Difference) (d) [3 points] XAY (Symmetric Difference)arrow_forward
- 4.2 Product and Quotient Rules 1. 9(x)=125+1 y14+2 Use the product and/or quotient rule to find the derivative of each function. a. g(x)= b. y (2x-3)(x-1) c. y== 3x-4 √xarrow_forward4.2 Product and Quotient Rules 1. Use the product and/or quotient rule to find the derivative of each function. 2.5 a. g(x)=+1 y14+2 √x-1) b. y=(2x-3)(x-:arrow_forwardFor what values of k will the equation (k + 1)x² + 6kx + 2k² - x = 0 have: a) one root equal zero b) one root the reciprocal of the other c) roots numerically equal but of opposite signarrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage


 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning





