Chapter 9.5, Problem 9.118P

(a)

To determine

Find the mass moment of inertia $\left(I_{CC\text{'}}\right)$ of the plate with respect to centroidal axis $CC\text{'}$ that is perpendicular to the plate.

Answer to Problem 9.118P

The mass moment of inertia $\left(I_{CC\text{'}}\right)$ of the plate with respect to centroidal axis $CC\text{'}$ that is perpendicular to the plate is $\underset{\_}{0.994m{a}^2}$.

Explanation of Solution

Given information:

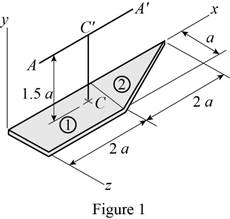
The height of the section is 1.5a.

The width of the section is a.

The length of the section up to straight edge is 2a.

The length of the section in sloped edge is 2a.

Calculation:

Let divide the section into 1 and 2.

Show the section 1 and section 2 as in Figure 1.

Calculate the area $\left(A_1\right)$ of the section 1 as below:

$\begin{array}{c}{A}_1=\left(2a\right)\left(a\right)\\ =2a^2\end{array}$

Calculate the area $\left(A_2\right)$ of the section 2 as below:

$\begin{array}{c}{A}_2=\frac{1}{2}\left(2a\right)\left(a\right)\\ =a^2\end{array}$

Calculate the value ${\left(\overline{x}A\right)}_1$ of the section 1 as below:

${\left(\overline{x}A\right)}_1=\frac{2a}{2}\times A_1$

Substitute $2a^2$ for $A_1$.

$\begin{array}{c}{\left(\overline{x}A\right)}_1=\frac{2a}{2}\times 2a^2\\ =2a^3\end{array}$

Calculate the value ${\left(\overline{x}A\right)}_2$ of the section 2 as below:

${\left(\overline{x}A\right)}_2=\left(2a+\frac{1}{3}2a\right)\times A_2$

Substitute $a^2$ for $A_2$.

$\begin{array}{c}{\left(\overline{x}A\right)}_2=\left(2a+\frac{1}{3}2a\right)\times a^2\\ =\frac{8}{3}{a}^3\end{array}$

Calculate the value ${\left(\overline{z}A\right)}_1$ of the section 1 as below:

${\left(\overline{z}A\right)}_1=\frac{1}{2}a\times A_1$

Substitute $2a^2$ for $A_1$.

$\begin{array}{c}{\left(\overline{z}A\right)}_1=\frac{1}{2}a\times 2a^2\\ =a^3\end{array}$

Calculate the value ${\left(\overline{z}A\right)}_2$ of the section 2 as below:

${\left(\overline{z}A\right)}_2=\left(\frac{1}{3}a\right)\times A_2$

Substitute $a^2$ for $A_2$.

$\begin{array}{c}{\left(\overline{z}A\right)}_2=\left(\frac{1}{3}a\right)\times a^2\\ =\frac{a^3}{3}\end{array}$

Calculate the centroid $\left(\overline{X}\right)$ of the trapezoidal plate with respect to z axis using the relation:

$\begin{array}{l}\overline{X}=\frac{{\displaystyle \sum \overline{x}A}}{{\displaystyle \sum A}}\\ \overline{X}=\frac{{\left(\overline{x}A\right)}_1+{\left(\overline{x}A\right)}_2}{A_1+A_2}\end{array}$

Substitute $2a^3$ for ${\left(\overline{x}A\right)}_1$, $\frac{8}{3}{a}^3$ for ${\left(\overline{x}A\right)}_2$, $2a^2$ for $A_1$ and $a^2$ for $A_2$.

$\begin{array}{c}\overline{X}=\frac{2a^3+\frac{8}{3}{a}^3}{2a^2+a^2}\\ =\frac{14}{9}a\end{array}$

Calculate the centroid $\left(\overline{Z}\right)$ of the trapezoidal plate with respect to x axis using the relation:

$\begin{array}{l}\overline{Z}=\frac{{\displaystyle \sum }}{{\displaystyle \sum A}}\\ \overline{Z}=\frac{{\left(\overline{z}A\right)}_1+{\left(\overline{z}A\right)}_2}{A_1+A_2}\end{array}$

Substitute $a^3$ for ${\left(\overline{z}A\right)}_1$, $\frac{a^3}{3}$ for ${\left(\overline{z}A\right)}_2$, $2a^2$ for $A_1$ and $a^2$ for $A_2$.

$\begin{array}{c}\overline{Z}=\frac{a^3+\frac{a^3}{3}}{2a^2+a^2}\\ =\frac{4}{9}a\end{array}$

Calculate the area (A) of the trapezoidal plate as below:

$\begin{array}{c}A=A_1+A_2\\ =2a^2+a^2\\ =3a^2\end{array}$

Express the mass (m) as below:

$m=\rho tA$

Here, $\rho$ is density and t thickness of the plate.

Rewrite the above equation as,

$\rho t=\frac{m}{A}$

Substitute $3a^2$ for A.

$\rho t=\frac{m}{3a^2}$

Express the mass moment of inertia $\left(I_{\text{mass}}\right)$ as below:

$I_{\text{mass}}=\rho t{I}_{area}$

Substitute $\frac{m}{3a^2}$ for $\rho t$.

$I_{\text{mass}}=\frac{m}{3a^2}{I}_{area}$ (1)

Calculate the moment of inertia of area ${\left(I_{x,area}\right)}_1$ about x axis for section 1 as below:

$\begin{array}{c}{\left(I_{x,area}\right)}_1=\frac{1}{3}\left(2a\right)\left(a^3\right)\\ =\frac{2}{3}{a}^4\end{array}$

Calculate the moment of inertia of area ${\left(I_{x,area}\right)}_2$ about x axis for section 2 as below:

$\begin{array}{c}{\left(I_{x,area}\right)}_2=\frac{1}{12}\left(2a\right)\left(a^3\right)\\ =\frac{1}{6}{a}^4\end{array}$

Calculate the moment of inertia $\left(I_{x,\text{area}}\right)$ of area of trapezoidal plate with respect to x axis as below:

$I_{x,\text{area}}={\left(I_{x,\text{area}}\right)}_1+{\left(I_{x,\text{area}}\right)}_2$

Substitute $\frac{2}{3}{a}^4$ for ${\left(I_{x,area}\right)}_1$ and $\frac{1}{6}{a}^4$ for ${\left(I_{x,area}\right)}_2$.

$\begin{array}{c}{I}_{x,\text{area}}=\frac{2}{3}{a}^4+\frac{1}{6}{a}^4\\ =\frac{5}{6}{a}^4\end{array}$

Calculate the mass moment of inertia $\left(I_{x,\text{mass}}\right)$ of trapezoidal plate with respect to x axis as below:

Rewrite the equation (1) as,

$I_{x,\text{mass}}=\frac{m}{3a^2}{I}_{x,area}$

Substitute $\frac{5}{6}{a}^4$ for $I_{x,area}$.

$\begin{array}{c}{I}_{x,\text{mass}}=\frac{m}{3a^2}\times \frac{5}{6}{a}^4\\ =\frac{5}{18}m{a}^2\end{array}$

Calculate the moment of inertia of area ${\left(I_{z,area}\right)}_1$ about z axis for section 1 as below:

$\begin{array}{c}{\left(I_{z,area}\right)}_1=\frac{1}{3}\left(a\right){\left(2a\right)}^3\\ =\frac{8}{3}{a}^4\end{array}$

Calculate the centroid $\left(\overline{x}\right)$ of the section 2 with respect to z axis as below:

$\overline{x}=2a+\frac{1}{3}\times 2a$

Express the moment of inertia $\left(I_{z\text{'}}\right)$ of section to about z axis as below:

$I_{z\text{'}}=\frac{1}{36}\left(a\right){\left(2a\right)}^3$

Calculate moment of inertia of area ${\left(I_{z,area}\right)}_2$ about z axis for section 2 using the relation:

${\left(I_{z,area}\right)}_2=I_{z\text{'}}+A_2{\overline{x}}^2$

Substitute $\frac{1}{36}\left(a\right){\left(2a\right)}^3$ for $I_{z\text{'}}$, $\frac{1}{2}\left(2a\right)\left(a\right)$ for $A_2$ and $2a+\frac{1}{3}\times 2a$ for $\overline{x}$.

$\begin{array}{c}{\left(I_{z,area}\right)}_2=\frac{1}{36}\left(a\right){\left(2a\right)}^3+\left(\frac{1}{2}\left(2a\right)\left(a\right)\right)\times {\left(2a+\frac{1}{3}\times 2a\right)}^2\\ =\frac{8}{36}{a}^4+\left(a^2\times {\left(\frac{8}{3}a\right)}^2\right)\\ =\frac{8}{36}{a}^4+\left(\frac{64}{9}{a}^4\right)\end{array}$

Calculate the moment of inertia $\left(I_{x,\text{area}}\right)$ of area of trapezoidal plate with respect to z axis as below:

$I_{z,\text{area}}={\left(I_{z,\text{area}}\right)}_1+{\left(I_{z,\text{area}}\right)}_2$

Substitute $\frac{8}{3}{a}^4$ for ${\left(I_{z,area}\right)}_1$ and $\frac{8}{36}{a}^4+\left(\frac{64}{9}{a}^4\right)$ for ${\left(I_{z,area}\right)}_2$.

$\begin{array}{c}{I}_{z,\text{area}}=\frac{8}{3}{a}^4+\frac{8}{36}{a}^4+\left(\frac{64}{9}{a}^4\right)\\ =10a^4\end{array}$

Calculate the mass moment of inertia $\left(I_{z,\text{mass}}\right)$ of trapezoidal plate with respect to z axis as below:

Rewrite the equation (1) as,

$I_{\text{z,mass}}=\frac{m}{3a^2}{I}_{z,area}$

Substitute $10a^4$ for $I_{x,area}$.

$\begin{array}{c}{I}_{\text{z,mass}}=\frac{m}{3a^2}\times 10a^4\\ =\frac{10}{3}m{a}^2\end{array}$

Calculate the mass moment of inertia $\left(I_{y,\text{mass}}\right)$ of trapezoidal plate with respect to y axis as below:

$I_{y,\text{mass}}=I_{x,\text{mass}}+I_{z,\text{mass}}$

Substitute $\frac{10}{3}m{a}^2$ for $I_{\text{z,mass}}$ and $\frac{5}{18}m{a}^2$ for $I_{x,\text{mass}}$.

$\begin{array}{c}{I}_{y,\text{mass}}=\frac{5}{18}m{a}^2+\frac{10}{3}m{a}^2\\ =\frac{65}{18}m{a}^2\end{array}$

Write the expression for mass moment of inertia $\left(I_{y,\text{mass}}\right)$ with respect to y axis as below:

$I_{y,\text{mass}}=I_{CC\text{'},\text{mass}}+m\left({\overline{X}}^2+{\overline{Z}}^2\right)$

Rewrite the above equation as,

$I_{CC\text{'},\text{mass}}=I_{y,\text{mass}}-m\left({\overline{X}}^2+{\overline{Z}}^2\right)$ (2)

Calculate the mass moment of inertia $\left(I_{CC\text{'}}\right)$ of the plate with respect to centroidal axis $CC\text{'}$ that is perpendicular to the plate as below:

Substitute $\frac{65}{18}m{a}^2$ for $I_{y,\text{mass}}$, $\frac{14}{9}a$ for $\overline{X}$ and $\frac{4}{9}a$ for $\overline{Z}$ in equation (2).

$\begin{array}{c}{I}_{CC\text{'},\text{mass}}=\frac{65}{18}m{a}^2-m\left({\left(\frac{14}{9}a\right)}^2+{\left(\frac{4}{9}a\right)}^2\right)\\ =\frac{65}{18}m{a}^2-\frac{212}{81}m{a}^2\\ =0.994m{a}^2\end{array}$

Therefore, the mass moment of inertia $\left(I_{CC\text{'}}\right)$ of the plate with respect to centroidal axis $CC\text{'}$ that is perpendicular to the plate is $\underset{\_}{0.994m{a}^2}$.

(b)

To determine

The mass moment of inertia $\left(I_{y,\text{mass}}\right)$ of the plate with respect to axis $AA\text{'}$ that is parallel to the x axis and is located at a distance 1.5a from the plate.

Answer to Problem 9.118P

The mass moment of inertia $\left(I_{y,\text{mass}}\right)$ of the plate with respect to axis $AA\text{'}$ that is parallel to the x axis and is located at a distance 1.5a from the plate is $\underset{\_}{2.33m{a}^2}$.

Explanation of Solution

Given information:

The height of the section is 1.5a.

The width of the section is a.

The length of the section up to straight edge is 2a.

The length of the section in sloped edge is 2a.

Calculation:

Write the expression for mass moment of inertia $\left(I_{x,\text{mass}}\right)$ with respect to x axis as below:

$\begin{array}{c}\left(I_{x,\text{mass}}\right)=I_{BB\text{'},\text{mass}}+m\left({\overline{Z}}^2\right)\\ I_{BB\text{'},\text{mass}}=I_{x,\text{mass}}-m\left({\overline{Z}}^2\right)\end{array}$ (3)

Calculate the mass moment of inertia $\left(I_{AA\text{'},\text{mass}}\right)$ with respect to $AA\text{'}$ axis as below:

$I_{AA\text{'},\text{mass}}=I_{BB\text{'},\text{mass}}+m{\left(1.5a\right)}^2$

Substitute $I_{x,\text{mass}}-m\left({\overline{Z}}^2\right)$ for $I_{BB\text{'},\text{mass}}$.

$\begin{array}{c}{I}_{AA\text{'},\text{mass}}=\left(I_{x,\text{mass}}-m\left({\overline{Z}}^2\right)\right)+m{\left(1.5a\right)}^2\\ I_{AA\text{'},\text{mass}}=I_{x,\text{mass}}+m\left({\left(1.5a\right)}^2-\left({\overline{Z}}^2\right)\right)\end{array}$

Substitute $\frac{5}{18}m{a}^2$ for $I_{x,\text{mass}}$ and $\frac{4}{9}a$ for $\overline{Z}$.

$\begin{array}{c}{I}_{AA\text{'},\text{mass}}=\frac{5}{18}m{a}^2+m\left({\left(1.5a\right)}^2-{\left(\frac{4}{9}a\right)}^2\right)\\ =\frac{5}{18}m{a}^2+m\left(2.05a^2\right)\\ =2.33m{a}^2\end{array}$

Therefore, the mass moment of inertia $\left(I_{y,\text{mass}}\right)$ of the plate with respect to axis $AA\text{'}$ that is parallel to the x axis and is located at a distance 1.5a from the plate is $\underset{\_}{2.33m{a}^2}$.