Chapter 9.4, Problem 52E

Solution

To explain: The claim implies that the harmonic series must diverge and graph the sequence of partial.

The obtained terms is 0, 1, 2, 3, 4, 5, and 60.

Given Information:

The sequence is defined as,

  $1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots +\frac{1}{n}+\cdots$

Explanation:

Consider the given information,

  $1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots +\frac{1}{n}+\cdots$

First make the table of the partial sums of the given sequence.

$\frac{1}{n}$	Partial sum
1	1
2	$1.5$
3	$1.833$
4	$2.0833$
5	$2.283$
6	$2.45$
7	$2.5929$
8	$2.7179$

Now, draw the graph of $y=\ln x$ and above table on the plane.

  

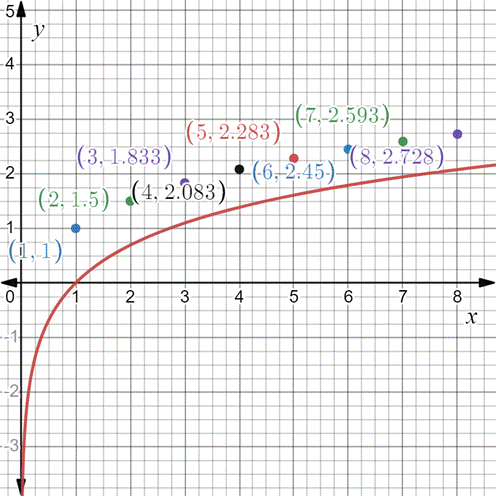
It can be seen that all points appear to lie above the function  $f\left(x\right)=\ln x$ , which implies that  $a_n\ge f\left(n\right)$ .

  $\begin{array}{c}{a}_n=1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}\\ \ge \ln n\end{array}$

Since the function  $f\left(x\right)=\ln x$  is not bounded as  $x\to \infty$ , $a_n$ cannot be bounded as  $n\to +\infty$ either as  $a_n$ is larger than  $f\left(n\right)$  at all times.

Hence, the function $f\left(x\right)=\ln x$ is not bounded as the limit tends to infinity.