Chapter 9.2, Problem 42E

Solution

a.

To find: The positive integer appears the least number of times.

The positive integer appears the least number of times is $2$ .

Given information:

Consider the patterns in Pascal’s triangle.

Calculation:

The Pascal’s triangle is given by,

  

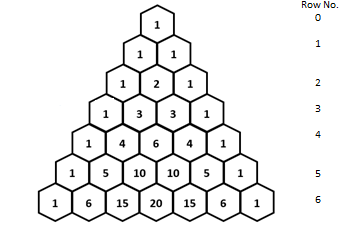
The smallest number that is not $1$ will be the least common positive number since the number $1$ repeats but all other numbers grow larger as you move down Pascal's triangle.

Therefore, the positive integer appears the least number of times is $2$ .

b.

To find: The numbers that appears the greatest number of times.

The numbers that appears the greatest number of times is $1$ .

Given information:

Consider the patterns in Pascal’s triangle.

Calculation:

The Pascal’s triangle is given by,

  

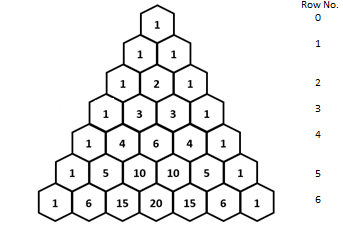
The number $1$ will be the most common because it makes up the edges of Pascal's triangle.

Therefore, the numbers that appears the greatest number of times is $1$ .

c.

To find: Whether any positive integer that does not appear in Pascal’s triangle?

Every positive integer appears in the Pascal’s triangle.

Given information:

Consider the patterns in Pascal’s triangle.

Calculation:

The Pascal’s triangle is given by,

  

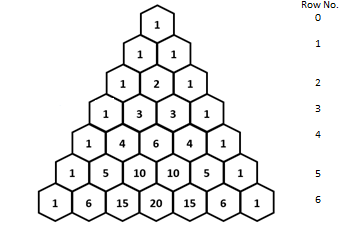
Every positive number will increase by one because the edges are formed of $1$ , hence every positive integer will appear on the Pascal's triangle.

Therefore, every positive integer appears in the Pascal’s triangle.

d.

To find: The result when adding and subtracting in any row.

The result when adding and subtracting in any row is equals to $2$ .

Given information:

Consider the patterns in Pascal’s triangle.

Calculation:

The Pascal’s triangle is given by,

  

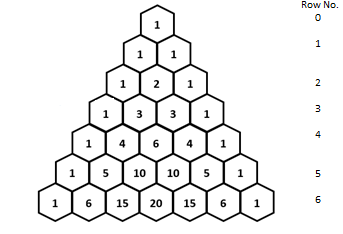
The numbers are identical on both sides if you cut the Pascal triangle in half down the middle.

As a result, the $1\text{'}\text{s}$ on both edges will remain because the numbers cancel each other out.

Thus,

  $1+1=2$

So, all row adds up to $2$ .

Therefore, the result when adding and subtracting in any row is equals to $2$ .

e.

To find: The interior numbers along the $p\text{th}$ row have in common.

The interior numbers along the $p\text{th}$ row have in common is a multiple of $p$ .

Given information:

Consider the patterns in Pascal’s triangle.

Calculation:

The Pascal’s triangle is given by,

  

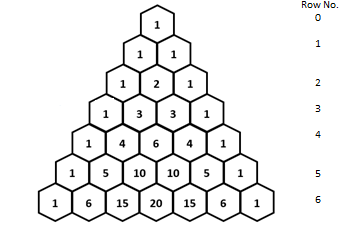
If the number were prime, $p$ , then every interior number on that row will be a multiple of $p$ since the Pascal's triangle uses what is above it to find the following row.

Therefore, the interior numbers along the $p\text{th}$ row have in common is a multiple of $p$ .

f.

To find: The rows that have all even interior numbers.

The rows that have all even interior numbers when the number is ${\text{2}}^x$ .

Given information:

Consider the patterns in Pascal’s triangle.

Calculation:

The Pascal’s triangle is given by,

  

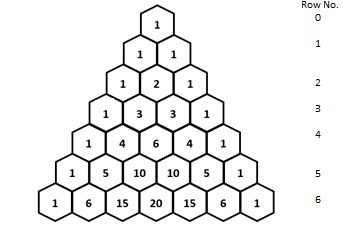
The row number must be a number that is ${\text{2}}^x$ in order for the interior of the row to contain only even numbers.

Therefore, the rows that have all even interior numbers when the number is ${\text{2}}^x$ .

g.

To find: The rows that have all odd numbers.

The rows that have all odd numbers when it does not follow ${\text{2}}^x$ .

Given information:

Consider the patterns in Pascal’s triangle.

Calculation:

The Pascal’s triangle is given by,

  

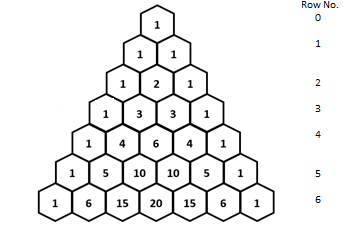
From part (f) it is known that the even interior numbers will follow ${\text{2}}^x$ .

So, the odd interior number will not follow ${\text{2}}^x$

  $\left(2,4,8,16,\mathrm{32....}\right)$ .

Therefore, the rows that have all odd numbers when it does not follow ${\text{2}}^x$ .

h.

To find: The other patterns in the Pascal’s triangle.

The other pattern obtained is a sum of ${\text{2}}^{n-1}$ .

Given information:

Consider the patterns in Pascal’s triangle.

Calculation:

The Pascal’s triangle is given by,

  

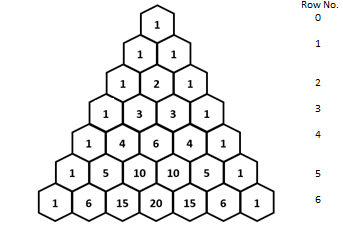
The top of Pascal's triangle has a $1$ , and its left and right edges also have one. The two numbers above the location can be added to get the other values in the triangle, which implies that Pascal's equality.

  $\left(\begin{array}{c}n+1\\ r\end{array}\right)=\left(\begin{array}{l}n\\ r\end{array}\right)+\left(\begin{array}{c}n\\ r-1\end{array}\right)$

Additionally, it is observed that the positive integers are found on the second diagonal, which is slanted and located next to the side of the Pascal's triangle that contains all ones.

By adding all the numbers in the $n\text{th}$ row, to get a sum of ${\text{2}}^{n-1}$ .

Therefore, the other pattern is found by adding all the numbers in the $n\text{th}$ row, to get a sum of ${\text{2}}^{n-1}$ .