Chapter 9.3, Problem 9.79P

Determine for the quarter ellipse of Prob. 9.67 the moments of inertia and the product of inertia with respect to new axes obtained by rotating the x and y axes about O (a) through 45° counterclockwise, (b) through 30° clockwise.

9.67 through 9.70 Determine by direct integration the product of inertia of the given area with respect to the x and y axes.

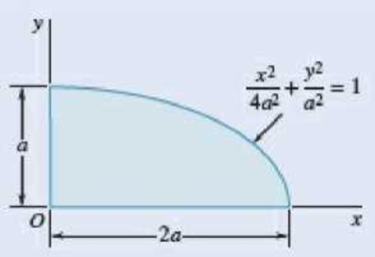
Fig. P9.67

To determine

Find the moment of inertia and product of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x and y axes about O through $45°$ clockwise.

Answer to Problem 9.79P

The moment of inertia for quarter ellipse with respect to new centroid axes obtained by rotating the x about O through $45°$ clockwise is $\underset{\_}{0.482a^4}$.

The moment of inertia for quarter ellipse with respect to new centroid axes obtained by rotating the y about O through $45°$ clockwise is $\underset{\_}{1.482a^4}$.

The product of inertia for quarter ellipse with respect to new centroid axes obtained by rotating the x and y about O through $45°$ clockwise is $\underset{\_}{-0.589a^4}$.

Explanation of Solution

Calculation:

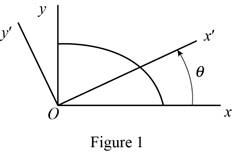
Sketch the quarter ellipse as shown in Figure 1.

Refer to Figure 9.12 “Moments of inertia of common geometric Shapes” in the textbook.

Find the moment of inertia $\left(I_x\right)$ for quarter ellipse as shown below:

$\left(I_x\right)=\frac{\pi }{16}\left(a{b}^3\right)$ (1)

Here, a is moments and products of area for a quarter of a circle of radius.

Substitute $2a$ for a and a for b in Equation (1).

$\begin{array}{c}\left(I_x\right)=\frac{\pi }{16}\left(2a\right){\left(a\right)}^3\\ =\frac{\pi }{16}2a^4\\ =\frac{\pi }{8}{a}^4\end{array}$

Find the moment of inertia $\left(I_y\right)$ for quarter ellipse as shown below:

$\left(I_y\right)=\frac{\pi }{16}\left(a^{3}b\right)$ (2)

Substitute $2a$ for a and a for b in Equation (2).

$\begin{array}{c}\left(I_y\right)=\frac{\pi }{16}{\left(2a\right)}^3\left(a\right)\\ =\frac{\pi }{16}8a^4\\ =\frac{\pi }{2}{a}^4\end{array}$

Refer to problem 9.67.

Write the curve Equation as shown below:

$\frac{x^2}{4a^2}+\frac{y^2}{a^2}=1$ (3)

Modify Equation (3).

$\begin{array}{l}\frac{x^2}{4a^2}+\frac{y^2}{a^2}=1\\ \frac{y^2}{a^2}=1-\frac{x^2}{4a^2}\\ \frac{y}{a}=\sqrt{1-\frac{x^2}{4a^2}}\\ y=a\sqrt{1-\frac{x^2}{4a^2}}\end{array}$

$y=\frac{1}{2}\sqrt{4a^2-x^2}$

Select a vertical strip as differential element of area.

Applying the parallel axis theorem.

$d{I}_{xy}=d{I}_{x^{\prime }{y}^{\prime }}+{\overline{x}}_{EL}{\overline{y}}_{EL}dA$

Here, ${\overline{x}}_{EL}$ and ${\overline{y}}_{EL}$ are the coordinates of the centroid of the element of area $dA$.

Using the property of symmetry about x and y axis.

$d{\overline{I}}_{x^{\prime }{y}^{\prime }}=0$

Express the variables in terms of x and y.

${\overline{x}}_{EL}=x$

Find the coordinate of centroid element ${\overline{y}}_{EL}$ as shown below:

${\overline{y}}_{EL}=\frac{1}{2}y$ (4)

Substitute $\frac{1}{2}\sqrt{4a^2-x^2}$ for y in Equation (4).

${\overline{y}}_{EL}=\frac{1}{2}\sqrt{4a^2-x^2}$

Consider the element strip as follows:

$\begin{array}{c}dA=ydx\\ =\frac{1}{2}\sqrt{4a^2-x^{2}dx}\end{array}$

Integrating $d{I}_x$ apply the limits as shown below:

$\begin{array}{c}{I}_{xy}={\displaystyle \int d{I}_{xy}}\\ ={\displaystyle \underset{0}{\overset{2a}{\int }}x\left(\frac{1}{4}\sqrt{4a^2-x^2}\right)\left(\frac{1}{2}\sqrt{4a^2-x^2}\right)}dx\\ =\frac{1}{8}{\displaystyle \underset{0}{\overset{2a}{\int }}\left(4a^{2}x-x^3\right)dx}\\ =\frac{1}{8}{\left[\frac{4a^2{x}^2}{2}-\frac{x^4}{4}\right]}_0^{2a}\end{array}$

$\begin{array}{c}=\frac{1}{8}\left[2a^2{\left(2a\right)}^2-\frac{{\left(2a\right)}^4}{4}\right]\\ =\frac{1}{8}\left[8a^4-4a^4\right]\\ =\frac{1}{8}\left[4a^4\right]\\ I_{xy}=\frac{1}{2}{a}^4\end{array}$

Find the value of $\frac{1}{2}\left(I_x+I_y\right)$:

$\begin{array}{c}\frac{1}{2}\left(I_x+I_y\right)=\frac{1}{2}\left(\frac{\pi }{8}{a}^4+\frac{\pi }{2}{a}^4\right)\\ =\frac{1}{2}{a}^4\left(\frac{\pi }{8}+\frac{\pi }{2}\right)\\ =\frac{1}{2}{a}^4\left(\frac{2\pi +8\pi }{16}\right)\\ =\frac{1}{2}{a}^4\left(\frac{10\pi }{16}\right)\end{array}$

$\frac{1}{2}\left(I_x+I_y\right)=\frac{5}{16}\pi a^4$

Find the value of $\frac{1}{2}\left(I_x-I_y\right)$:

$\begin{array}{c}\frac{1}{2}\left(I_x-I_y\right)=\frac{1}{2}\left(\frac{\pi }{8}{a}^4-\frac{\pi }{2}{a}^4\right)\\ =\frac{1}{2}{a}^4\left(\frac{\pi }{8}-\frac{\pi }{2}\right)\\ =\frac{1}{2}{a}^4\left(\frac{2\pi -8\pi }{16}\right)\\ =\frac{1}{2}{a}^4\left(\frac{6\pi }{16}\right)\end{array}$

$\frac{1}{2}\left(I_x-I_y\right)=-\frac{3}{16}\pi a^4$

Find the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x about O through $45°$ clockwise using the Equation as follows:

Refer to Equation 9.18 in section 9.3B in the textbook.

$I_{x^{\prime }}=\frac{1}{2}\left(I_x+I_y\right)+\frac{1}{2}\left(I_x-I_y\right)\cos 2\theta -I_{xy}\sin 2\theta$ (5)

Substitute $\frac{5}{16}\pi a^4$ for $\frac{1}{2}\left(I_x+I_y\right)$, $\frac{3}{16}\pi a^4$ for $\frac{1}{2}\left(I_x-I_y\right)$, $\frac{1}{2}{a}^4$ for $I_{xy}$, and $45°$ for $\theta$ in Equation (5)

$\begin{array}{c}{I}_{x^{\prime }}=\frac{5}{16}\pi a^4-\frac{3}{16}\pi a^4\cos 2\left(45°\right)-\left(\frac{1}{2}{a}^4\right)\sin 2\left(45°\right)\\ =\frac{5}{16}\pi a^4-\frac{3}{16}\pi a^4\cos \left(90°\right)-\left(\frac{1}{2}{a}^4\right)\sin 90°\\ =a^4\left(\frac{5\pi }{16}-\frac{3\pi }{16}\left(0\right)-\frac{1}{2}\right)\\ =a^4\left(0.4817\right)\end{array}$

$I_{x^{\prime }}=0.482a^4$

Thus, the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x about O through $45°$ clockwise is $\underset{\_}{0.482a^4}$.

Find the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the y about O through $45°$ clockwise using the Equation as follows:

Refer to Equation 9.19 in section 9.3B in the textbook.

$I_{y^{\prime }}=\frac{1}{2}\left(I_x+I_y\right)-\frac{1}{2}\left(I_x-I_y\right)\cos 2\theta +I_{xy}\sin 2\theta$ (6)

Substitute $\frac{5}{16}\pi a^4$ for $\frac{1}{2}\left(I_x+I_y\right)$, $-\frac{3}{16}\pi a^4$ for $\frac{1}{2}\left(I_x-I_y\right)$, $\frac{1}{2}{a}^4$ for $I_{xy}$, and $45°$ for $\theta$ in Equation (6).

$\begin{array}{c}{I}_{y^{\prime }}=\frac{5}{16}\pi a^4-\left(-\frac{3}{16}\pi a^4\cos 2\left(45°\right)\right)+\frac{1}{2}{a}^4\sin 2\left(45°\right)\\ =\frac{5}{16}\pi a^4+\frac{3}{16}\pi a^4\cos 90°+\frac{1}{2}{a}^4\sin 90°\\ =a^4\left(\frac{5\pi }{16}+\frac{3\pi }{16}\left(0\right)+\frac{1}{2}\right)\\ =a^4\left(1.4817\right)\end{array}$

$I_{y^{\prime }}=1.482a^4$

Thus, the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the y about O through $45°$ clockwise is $\underset{\_}{1.482a^4}$.

Find the product of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x and y about O through $45°$ clockwise using the Equation as follows:

$I_{x^{\prime }{y}^{\prime }}=\frac{1}{2}\left(I_x-I_y\right)\sin 2\theta +I_{xy}\cos 2\theta$ (7)

Substitute $-\frac{3}{16}\pi a^4$ for $\frac{1}{2}\left(I_x-I_y\right)$, $\frac{1}{2}{a}^4$ for $I_{xy}$, and $45°$ for $\theta$ in Equation (7).

$\begin{array}{c}{I}_{x^{\prime }{y}^{\prime }}=-\frac{3}{16}\pi a^4\sin 2\left(45°\right)+\left(\frac{1}{2}{a}^4\right)\cos 2\left(45°\right)\\ =-\frac{3}{16}\pi a^4\sin 90°+\left(\frac{1}{2}{a}^4\right)\cos 90°\\ =a^4\left(-\frac{3}{16}\pi \right)\\ I_{x^{\prime }{y}^{\prime }}=-0.589a^4\end{array}$

Thus, the product of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x and y about O through $45°$ clockwise is $\underset{\_}{-0.589a^4}$.

To determine

Find the moment of inertia and product of inertia with respect new centroid axes obtained by rotating the x and y axes about O through $-30°$ clockwise.

Answer to Problem 9.79P

The moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x about O through $30°$ clockwise is $\underset{\_}{1.120a^4}$.

The moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the y about O through $30°$ clockwise is $\underset{\_}{0.834a^4}$.

The product of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x and y about O through $30°$ clockwise is $\underset{\_}{0.760a^4}$.

Explanation of Solution

Calculation:

Find the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x about O through $30°$ clockwise using the Equation as follows:

Refer to Equation 9.18 in section 9.3B in the textbook.

$I_{x^{\prime }}=\frac{1}{2}\left(I_x+I_y\right)+\frac{1}{2}\left(I_x-I_y\right)\cos 2\theta -I_{xy}\sin 2\theta$ (8)

Substitute $\frac{5}{16}\pi a^4$ for $\frac{1}{2}\left(I_x+I_y\right)$, $-\frac{3}{16}\pi a^4$ for $\frac{1}{2}\left(I_x-I_y\right)$, $\frac{1}{2}{a}^4$ for $I_{xy}$, and $-30°$ for $\theta$ in Equation (8).

$\begin{array}{c}{I}_{x^{\prime }}=\frac{5}{16}\pi a^4-\frac{3}{16}\pi a^4\cos 2\left(-30°\right)-\left(\frac{1}{2}{a}^4\right)\sin 2\left(-30°\right)\\ =\frac{5}{16}\pi a^4-\frac{3}{16}\pi a^4\cos \left(-60°\right)-\left(\frac{1}{2}{a}^4\right)\sin \left(-60°\right)\\ =a^4\left(\frac{5\pi }{16}-\frac{3\pi }{16}\left(-0.5\right)-\frac{1}{2}\left(-0.866\right)\right)\\ =1.120a^4\end{array}$

Thus, the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x about O through $30°$ clockwise is $\underset{\_}{1.120a^4}$.

Find the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the y about O through $30°$ clockwise using the Equation as follows:

Refer to Equation 9.19 in section 9.3B in the textbook.

$I_{y^{\prime }}=\frac{1}{2}\left(I_x+I_y\right)-\frac{1}{2}\left(I_x-I_y\right)\cos 2\theta +I_{xy}\sin 2\theta$ (9)

Substitute $\frac{5}{16}\pi a^4$ for $\frac{1}{2}\left(I_x+I_y\right)$, $-\frac{3}{16}\pi a^4$ for $\frac{1}{2}\left(I_x-I_y\right)$, $\frac{1}{2}{a}^4$ for $I_{xy}$, and $-30°$ for $\theta$ in Equation (9).

$\begin{array}{c}{I}_{y^{\prime }}=\frac{5}{16}\pi a^4+\frac{3}{16}\pi a^4\cos 2\left(-30°\right)+\frac{1}{2}{a}^4\sin 2\left(-30°\right)\\ =\frac{5}{16}\pi a^4+\frac{3}{16}\pi a^4\cos \left(-60°\right)+\frac{1}{2}{a}^4\sin \left(-60°\right)\\ =a^4\left(\frac{5\pi }{16}+\frac{5\pi }{16}\left(-0.5\right)+\frac{1}{2}\left(-0.866\right)\right)\\ =0.843a^4\end{array}$

Thus, the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the y about O through $30°$ clockwise is $\underset{\_}{0.834a^4}$.

Find the product of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x and y about O through $30°$ clockwise using the Equation as follows:

$I_{x^{\prime }{y}^{\prime }}=\frac{1}{2}\left(I_x-I_y\right)\sin 2\theta +I_{xy}\cos 2\theta$ (10)

Substitute $-\frac{3}{16}\pi a^4$ for $\frac{1}{2}\left(I_x-I_y\right)$, $\frac{1}{2}{a}^4$ for $I_{xy}$, and $-30°$ for $\theta$ in Equation (10).

$\begin{array}{c}{I}_{x^{\prime }{y}^{\prime }}=-\frac{3}{16}\pi a^4\sin 2\left(-30°\right)+\left(\frac{1}{2}{a}^4\right)\cos 2\left(-30°\right)\\ =-\frac{3}{16}\pi a^4\sin \left(-60°\right)+\left(\frac{1}{2}{a}^4\right)\cos \left(-60°\right)\\ =a^4\left(-\frac{3\pi }{16}\left(0.866\right)+\frac{1}{2}\left(-0.5\right)\right)\\ I_{x^{\prime }{y}^{\prime }}=0.760a^4\end{array}$

Thus, the product of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x and y about O through $30°$ clockwise is $\underset{\_}{0.760a^4}$.